1. 문제

프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2. 풀이 과정
모든 취약지점을 점검하기 위해 필요한 최소 친구 수를 구하는 문제이다.
친구를 최대한 적게 투입해야하기 때문에 배치에 신경을 써야한다.
나는 처음에 세 가지 제한사항을 뒀다.
1. 이동범위가 큰 친구부터 투입
일단 이동범위가 큰 친구부터 투입을 해야 최대한 많은 취약 지점을 한번에 수리할 수 있게 된다.
2. 시작은 무조건 취약 지점에서
취약 지점인 곳에서 시작을 하면 바로 한 곳을 수리하고 움직일 수 있다.
3. 가능한 케이스 중에서 가장 많은 곳을 수리할 수 있는 케이스를 선택하자.
아무래도 이동범위가 큰 친구가 많은 곳을 수리해 놔야 뒷 친구들이 남은 곳을 빠르게 수리할 확률이 높다고 생각했다.
하지만 이는 틀린 내용이다.
반례는 다음과 같다.
N: 50, weak: [1, 2, 3, 4, 5, 6, 30, 33, 36], dist: [6, 2, 2]
6만큼 움직이는 첫번째 친구가 가장 많은 곳을 수리하기 위해서 1에서 6으로 움직이게 되면 총 6곳을 수리할 수 있게 된다.
하지만 이렇게 되면 나머지 친구가 남은 곳을 모두 수리할 수 없게 된다.
반면 30에서 36으로 움직이게 되면 총 3곳밖에 수리를 못하지만 나머지 친구들이 1에서 3, 4에서 6으로 움직여서 모든 수리를 마칠 수 있게 된다. 이렇기 때문에 무조건 많은 곳을 수리한다고 좋은 것은 아니다.
이 세개 말고도 한 가지 알아둬야 할점이 있는데 바로 방향에 대한 부분이다.
해당 문제에서는 시계방향과 반시계 방향으로 움직일 수 있다고 했는데 이것이 함정이다.
결론부터 말하면 방향을 전혀 신경쓰지 않아도 된다.
다음 그림을 보자.
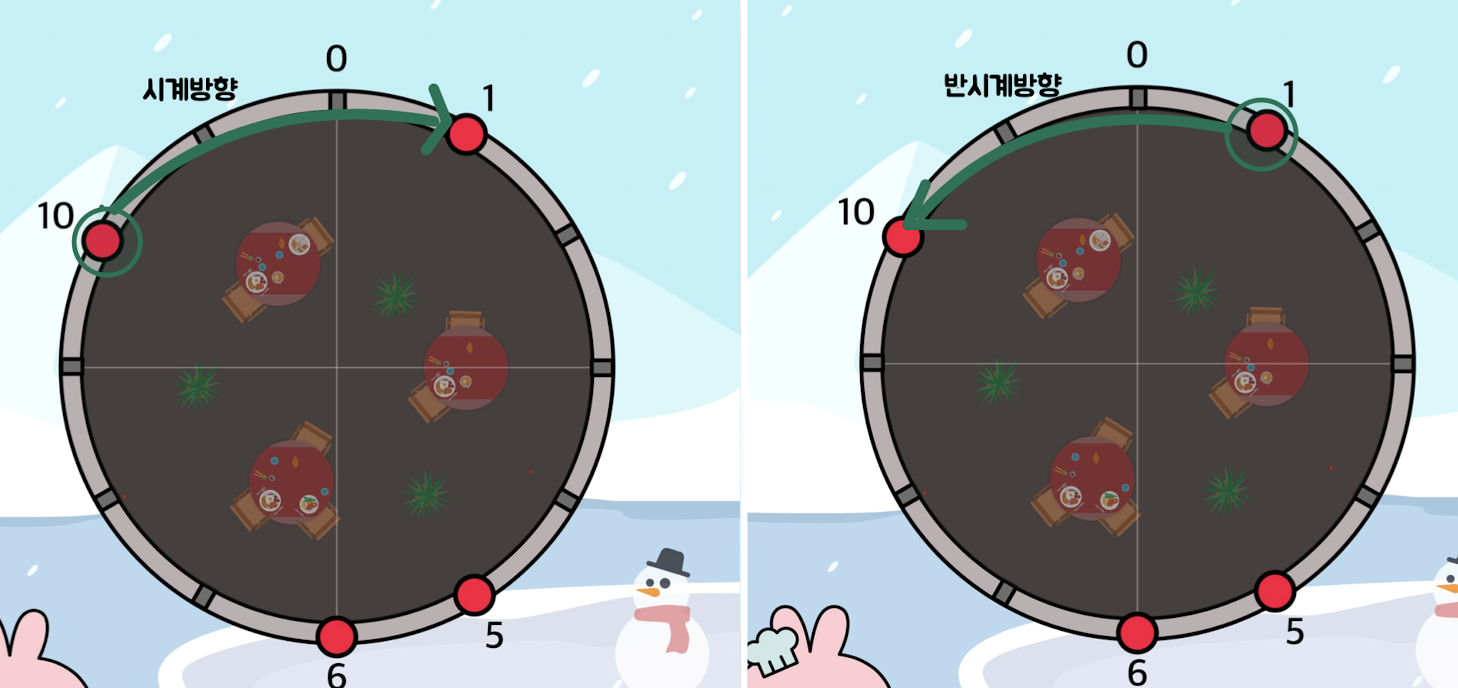
두 그림의 시작점은 10과 1로 각각 다르다. 하지만 같은 범위를 커버한다.
다시 말해 시계방향으로 갈 수 있는 범위는 반시계방향으로도 갈 수 있다는 의미이다.
그러므로 방향을 신경쓰지 않아도 된다.
이제 알고리즘을 짤 시간이다.
바로 코드를 보자.
3. 내 코드
import java.util.*;
class Solution {
private int[] Dist;
private int N;
private int min_fnd = Integer.MAX_VALUE;
public int solution(int n, int[] weak, int[] dist) {
// dist를 내림차순으로 정렬
Dist = dist;
N = n;
sortReverse(Dist);
List<Integer> weak_list = new ArrayList<>();
for(int i = 0; i < weak.length; i++) {
weak_list.add(weak[i]);
}
cntFriend(weak_list, 0);
return min_fnd != Integer.MAX_VALUE ? min_fnd: -1;
}
private void cntFriend(List<Integer> weak, int fnd_num) {
// 리턴조건1) 만약 weak 리스트가 비어있다면 모든 취약지점을 점검한 것
// 해당 케이스에서 보낸 친구 수 체크해서 현재 최솟값과 비교해서 더 작다면 갱신한다.
if(weak.isEmpty()){
if(min_fnd > fnd_num)
min_fnd = fnd_num;
return;
}
// 리턴조건2) 만약 fnd_num이 Dist의 길이와 같다면 모든 친구가 점검한 것
// weak 리스트가 비어있지 않는데도 모든 친구가 점검을 했다면 취약 지점을 전부 점검할 수 없는 케이스
// 리턴조건3) 만약 fnd_num이 min_fnd와 같다면 해당 케이스는 가능성이 없는 케이스
if(fnd_num == Dist.length || fnd_num == min_fnd)
return;
// 출발점을 취약점이 있는 곳으로 설정하여 점검하는 외벽을 제거 후 재귀 호출
for(int i = 0; i < weak.size(); i++) {
int start = weak.get(i); // 친구의 출발 지점
int end; // 친구의 도착 지점
// 시계 방향
List<Integer> newWeak = new ArrayList<>(weak);
end = start + Dist[fnd_num];
// 현재 친구가 점검한 외벽을 리스트에서 제거
for(int w: weak) {
if(end < N) {
if(w >= start && w <= end)
newWeak.remove(newWeak.indexOf(w));
} else {
if(w >= start || w <= end % N)
newWeak.remove(newWeak.indexOf(w));
}
}
// 제거한 리스트로 재귀 호출
cntFriend(newWeak, fnd_num + 1);
}
}
private void sortReverse(int[] dist) {
Integer[] distInteger = Arrays.stream(dist).boxed().toArray(Integer[]::new);
Arrays.sort(distInteger, Collections.reverseOrder());
for(int i = 0; i < distInteger.length; i++) {
dist[i] = distInteger[i];
}
}
}코드 설명
투입된 친구 수를 세기 위해서 재귀를 사용했다.
세 가지의 리턴조건을 설정했다.
// 리턴조건1) 만약 weak 리스트가 비어있다면 모든 취약지점을 점검한 것
// 해당 케이스에서 보낸 친구 수 체크해서 현재 최솟값과 비교해서 더 작다면 갱신한다.
if(weak.isEmpty()){
if(min_fnd > fnd_num)
min_fnd = fnd_num;
return;
}
// 리턴조건2) 만약 fnd_num이 Dist의 길이와 같다면 모든 친구가 점검한 것
// weak 리스트가 비어있지 않는데도 모든 친구가 점검을 했다면 취약 지점을 전부 점검할 수 없는 케이스
// 리턴조건3) 만약 fnd_num이 min_fnd와 같다면 해당 케이스는 가능성이 없는 케이스
if(fnd_num == Dist.length || fnd_num == min_fnd)
return;- 만약 weak 리스트가 비어있다면 모든 취약지점을 점검한 것
- 만약 fnd_num이 Dist의 길이와 같다면 모든 친구가 점검한 것
- 만약 fnd_num이 min_fnd와 같다면 해당 케이스는 가능성이 없는 케이스
출발점을 취약점이 있는 곳으로 설정하여 점검하는 외벽을 제거 후 다음 친구로 재귀호출했다.
// 출발점을 취약점이 있는 곳으로 설정하여 점검하는 외벽을 제거 후 재귀 호출
for(int i = 0; i < weak.size(); i++) {
int start = weak.get(i); // 친구의 출발 지점
int end; // 친구의 도착 지점
// 시계 방향
List<Integer> newWeak = new ArrayList<>(weak);
end = start + Dist[fnd_num];
// 현재 친구가 점검한 외벽을 리스트에서 제거
for(int w: weak) {
if(end < N) {
if(w >= start && w <= end)
newWeak.remove(newWeak.indexOf(w));
} else {
if(w >= start || w <= end % N)
newWeak.remove(newWeak.indexOf(w));
}
}
// 제거한 리스트로 재귀 호출
cntFriend(newWeak, fnd_num + 1);
}- 방향은 의미 없기때문에 임의로 시계방향으로 설정하였다
시간 복잡도
- O(w!*d)
취약 지점 리스트의 모든 가능한 순열을 시도하는 것이기 때문에 w!이 된다.
각 순열에 대해 최대 d번 재귀호출이 일어나므로 최종 시간 복잡도는 O(w!*d)가 된다.
'코딩 테스트 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 정수 내림차순으로 배치하기 (0) | 2024.06.20 |
|---|---|
| [프로그래머스] 문자열 내 마음대로 정렬하기 (0) | 2024.06.19 |
| [프로그래머스] 양궁 대회 (0) | 2024.06.14 |
| [프로그래머스] N-Queen (0) | 2024.06.14 |
| [프로그래머스] 피로도 (0) | 2024.06.14 |
