1. 문제

프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2. 풀이 과정
이 문제는 모든 칸을 방문하기 위해서 필요한 사다리 설치 비용의 최솟값을 구하는 문제이다.
이 문제에서 주의해야할 점은 현재 위치에서 인접한 위치로 당장 방문할 수 없다고 해서 그 위치를 방문할 수 없는 것이 아니다.
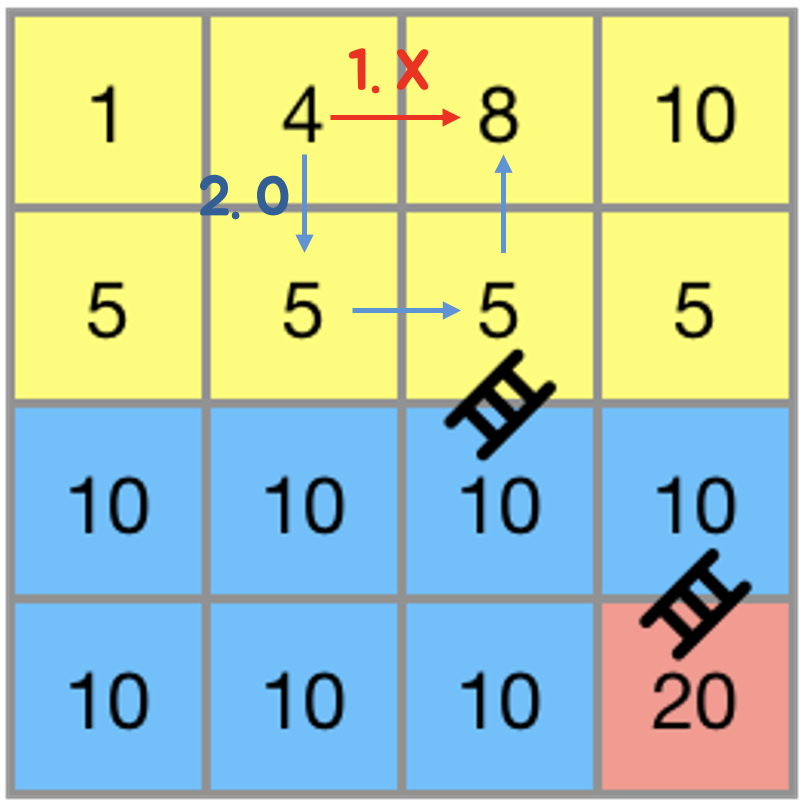
예를 들어 위의 케이스에서 최대 높이 차가 3이라고 할 때, (0, 2)에서 (1, 3)으로는 바로 갈 수가 없다.
그렇다고 해서 (1, 3)을 방문하지 못한다고 판단해 바로 사다리를 설치하면 안된다.
(0, 1) -> (1, 1) -> (1, 2) -> (0, 2)로 이동한다면 방문할 수 있기 때문이다.
따라서 다른 위치를 거쳐서도 못가는 경우에만 사다리를 설치해줘야 한다.
나는 이 문제를 해결하기 위해 다음과 같은 과정을 떠올렸다.
1. 0,0부터 인접한 곳 중 갈 수 있는 곳을 방문처리하고 큐에 넣음. 갈 수 없는 곳은 해시셋에 저장
일단 큐를 사용한 이유는 너비 우선 탐색을 위해서이다.
하지만 다른 점은 모든 인접한 노드를 큐에 넣는 것이 아닌 현재 갈 수 있는 곳만 큐에 넣어야 한다는 것이다.
그렇다고 해서 못가는 곳을 버리면 안된다. 다른 노드를 거쳐서라도 갈 수 있기 때문이다.
그래서 나는 별도의 자료구조에 저장하는 것이 좋다고 생각했고 아무래도 중복을 빠르게 걸러주는 해시셋이 좋다고 생각했다.
2. 큐에서 노드를 하나 꺼내 인접한 곳 중 갈 수 있는 곳을 방문처리하고 갈 수 없는 곳은 해시셋에 저장
근데 갈 수 있는 인접한 곳이 해시셋에 포함이 돼있다면 해당 위치를 해시셋에서 제외
큐에서 노드를 하나 꺼내 인접한 곳 중 갈 수 있는 곳을 방문처리하고 갈 수 없는 곳은 해시셋에 저장하는 것은 앞선 과정과 똑같다.
다른 건 갈 수 있는 인접한 곳이 해시셋에 포함이 돼있다면 해당 위치를 해시셋에서 제외시켜야 한다는 것이다.
이 과정이 필요한 이유는 바로 이전 노드에선 당장 갈 수 없어서 해당 노드를 해시 셋에 넣어놨지만 현재 노드를 거쳐서 가면 갈 수 있는 곳이 되기 때문이다.
3. 그렇게 큐가 비어있을때까지 반복
이 과정을 반복하게 되면 방문할 수 있는 노드들이 방문처리 될 것이다.
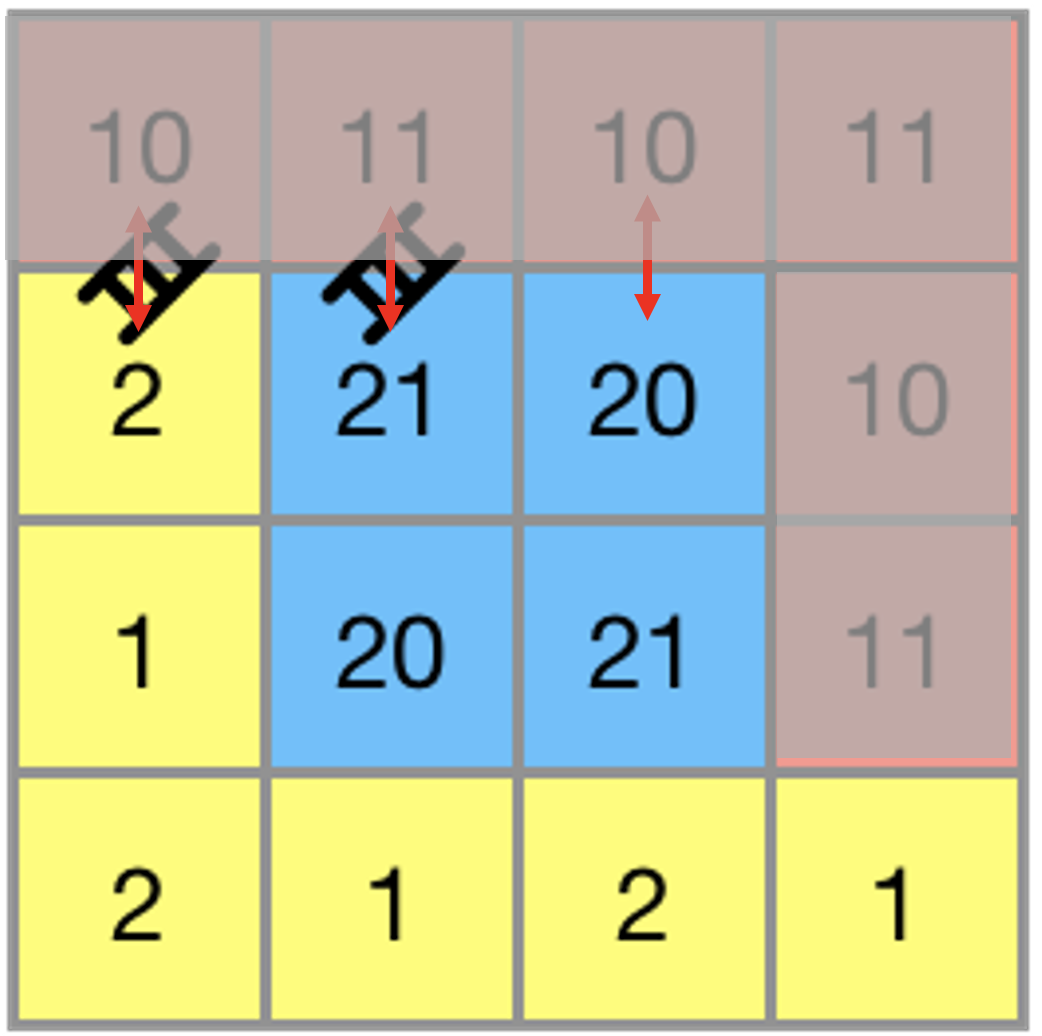
해당 예시에서 1~2의 과정을 거치면 위와 같다.
4. 해시 셋의 저장된 갈 수 없는 노드들을 하나씩 보면서 그 곳과 인접한 방문노드와의 높이차가 최소인 곳을 찾아 그 위치를 방문처리하고 비용을 업데이트한다. 또한 그 위치를 해시셋에 제외
1~3의 과정을 거치면 해시셋에는 다른 위치를 거쳐서도 못가는 노드만 남게 된다.
이제 다른 위치를 거쳐서도 못가는 노드 중 하나에 사다리를 놔야한다.
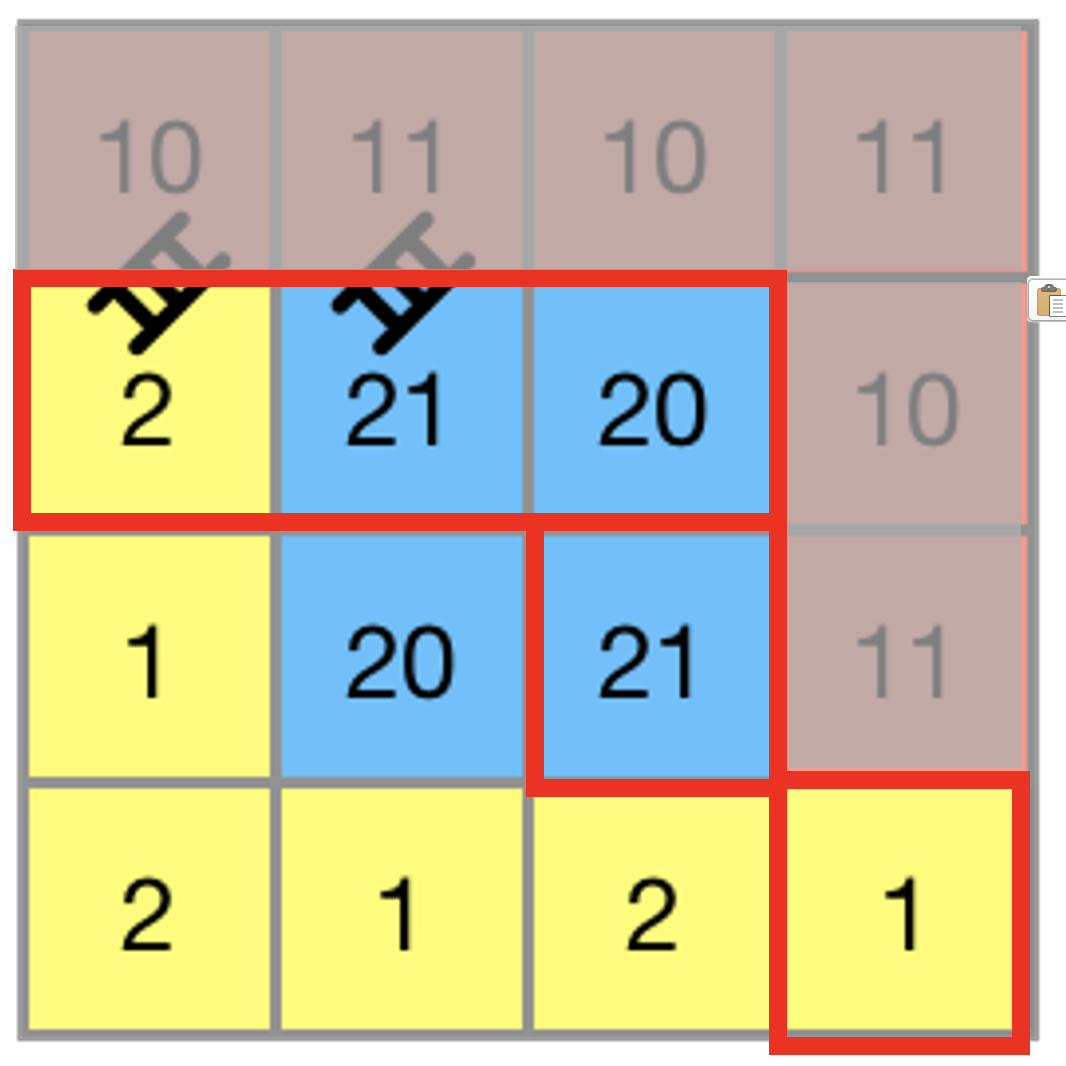
해당 예시에서 1~3의 과정을 거치면 빨간 네모로 표시된 다섯 곳이 해시셋에 들어갈 것이다.
여기서 각 노드에서 인접한 방문노드와의 높이차를 구한다.
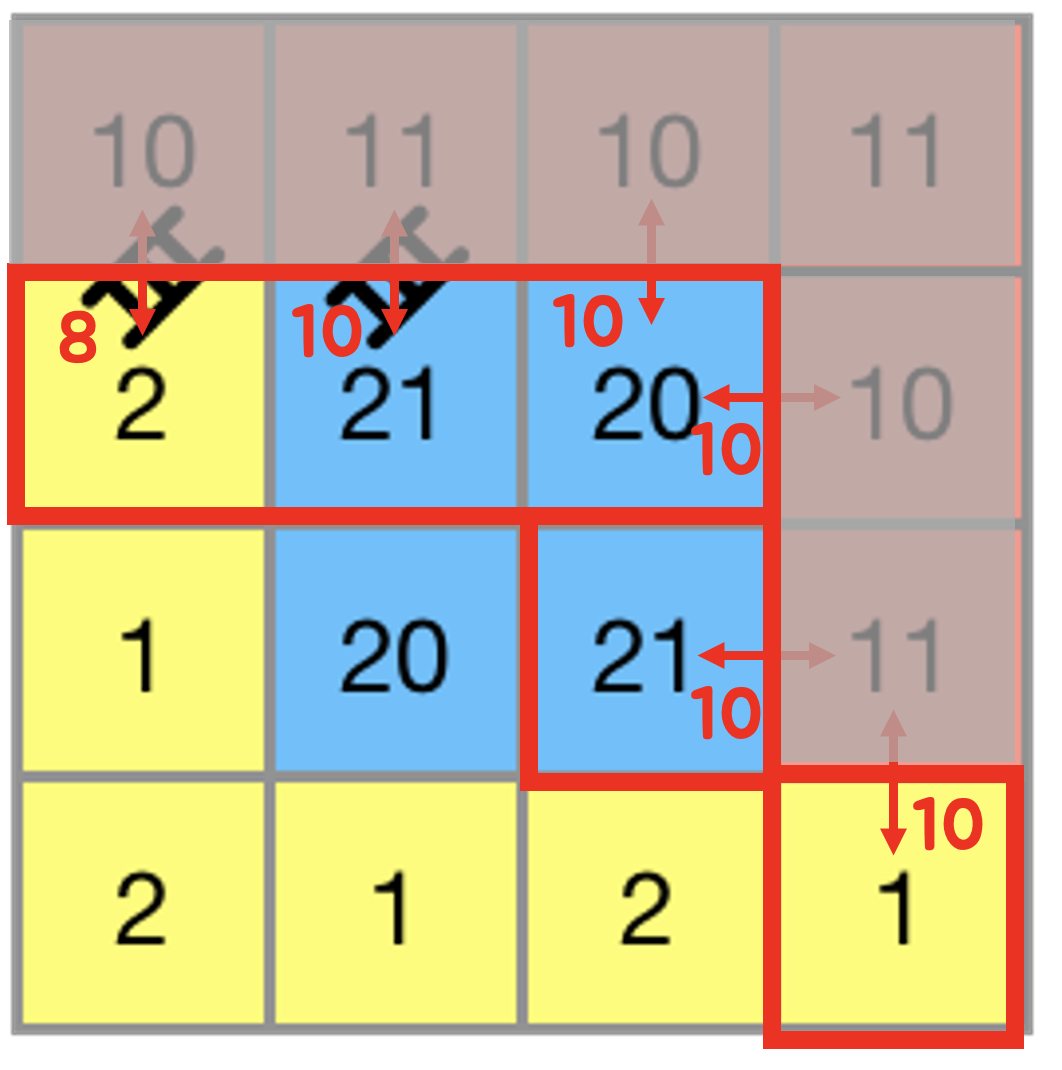
그러면 다음과 같은 결과가 나온다.
이때 최솟값은 8이고 해당 노드는 (1, 0)이다
해당 노드를 해시 셋에서 제거하고 해당 위치를 방문처리한다.
또한 비용을 8로 업데이트한다.
5. 사다리를 놓은 곳을 기준으로 1~4의 과정을 모든 위치가 방문처리 될때까지 반복한다.
3까지의 과정을 거쳤는데 해시셋의 값이 아무것도 없으면 모든 위치가 방문처리가 된 것이다.
이렇게 생각하고 코드를 구현해서 제출을 했다.
코드보기 ⬇️
import java.util.*;
class Solution {
static class Place {
int r; int c;
Place(int r, int c) {
this.r = r;
this.c = c;
}
@Override
public int hashCode() {
return Objects.hash(r, c);
}
@Override
public boolean equals(Object obj) {
if (this == obj) return true; // 같은 객체를 가리키는 경우 true 반환
if (obj == null || getClass() != obj.getClass()) return false; // null이거나 클래스 타입이 다른 경우 false 반환
Place place = (Place) obj; // obj를 Person 타입으로 캐스팅
return r == place.r && Objects.equals(c, place.c); // age와 name 필드를 비교
}
}
private static final int[] mr = {0, 0, 1, -1};
private static final int[] mc = {1, -1, 0, 0};
private int[][] Land;
private boolean[][] visited;
public int solution(int[][] land, int height) {
Land = land;
visited = new boolean[land.length][land[0].length];
Queue<Place> queue = new ArrayDeque<>();
Set<Place> cantGoSet = new HashSet<>();
int h = height;
int cost = 0;
int start_row = 0;
int start_col = 0;
while (true) {
Place start = new Place(start_row, start_col); // 0,0 부터 시작
queue.add(start);
visited[start.r][start.c] = true;
while (!queue.isEmpty()) {
Place place = queue.poll();
// 인접한 곳 중 갈 수 있는 곳은 방문처리하고 큐에 넣기
// 갈 수 없는 곳은 해시셋 저장
for (int i = 0; i < 4; i++) {
int nr = place.r + mr[i];
int nc = place.c + mc[i];
// 범위에서 벗어나는 경우 패스
if (isOutOfBounds(nr, nc))
continue;
// 현재 위치와 인접한 곳의 높이차가 최대 높이차 h보다 크지 않다면 갈 수 있는 곳
// 단 방문한 곳은 제외
if (!visited[nr][nc] && Math.abs(Land[place.r][place.c] - Land[nr][nc]) <= h) {
queue.add(new Place(nr, nc)); // 큐에 넣기
visited[nr][nc] = true; // 방문처리
cantGoSet.remove(new Place(nr, nc)); // 해당 위치가 기존에 갈 수 없던 곳이었다면 해당 위치를 해시셋에서 삭제
}
// 갈 수 없는 곳이라면 해시셋에 저장
else {
if(!visited[nr][nc])
cantGoSet.add(new Place(nr, nc));
}
}
}
// 만약 더 이상 방문할 수 없는 곳이 없다면 종료
if (cantGoSet.isEmpty())
break;
// 갈 수 없는 곳 중에서 그 곳과 인접하고 방문한 곳과의 높이차가 최소인 갈 수 없는 곳을 찾기
int min = Integer.MAX_VALUE;
int minr = -1;
int minc = -1;
for (Place p : cantGoSet) {
for (int i = 0; i < 4; i++) {
int nr = p.r + mr[i];
int nc = p.c + mc[i];
// 범위에서 벗어나는 경우 패스
if (isOutOfBounds(nr, nc))
continue;
// 해당 위치가 방문한 곳인 경우만 체크
if (visited[nr][nc]) {
if (min > Math.abs(Land[p.r][p.c] - Land[nr][nc])) {
min = Math.abs(Land[p.r][p.c] - Land[nr][nc]);
minr = p.r;
minc = p.c;
}
}
}
}
// 그 위치를 방문처리하고 그 높이차의 최소를 비용에 업데이트. 또한 그 위치를 해시셋에서 제외
visited[minr][minc] = true;
cost += min;
cantGoSet.remove(new Place(minr, minc));
// 그 위치를 시작 위치로 재설정
start_row = minr;
start_col = minc;
}
return cost;
}
private boolean isOutOfBounds(int row, int col) {
return row < 0 || row >= Land.length || col < 0 || col >= Land[0].length;
}
}
하지만 결과는
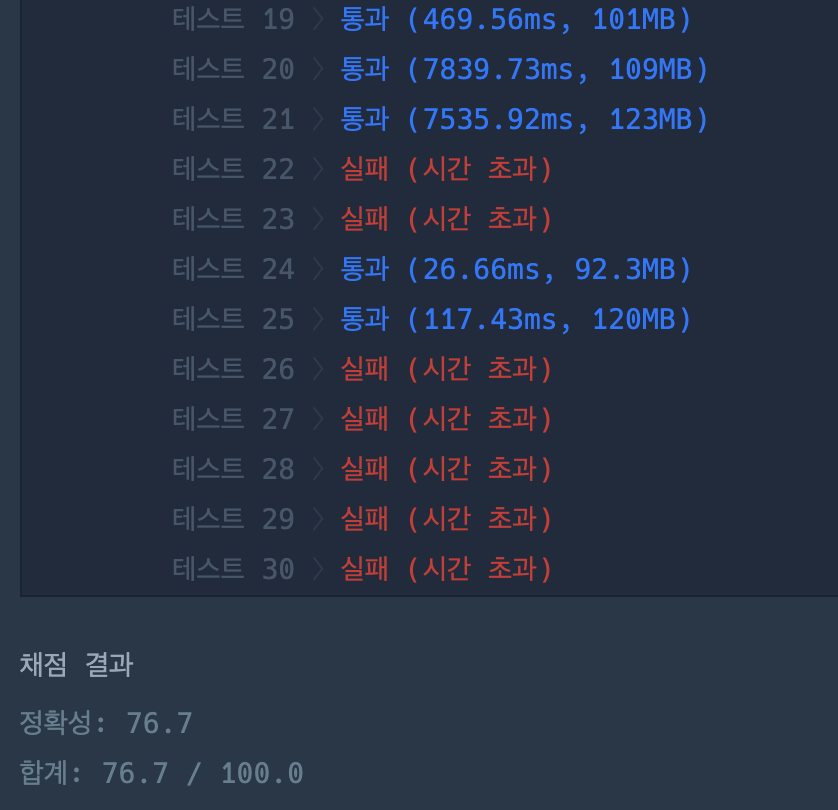
로직은 맞았는데 코드가 효율적이지 못하다는 것이다.
해결방안은 우선순위 큐이다.
우선순위 큐는 기존 큐와는 다르게 원하는 순서로 poll()을 할 수 있는 큐이다.
우선순위 큐를 활용해서 문제를 해결하는 과정은 다음과 같다.
1. (0,0)부터 인접한 곳 중 방문할 수 있는 곳은 cost를 0으로 설정하여 우선순위 큐에 저장한다. 방문할 수 없는 곳은 cost를 그 차이로 하여 우선순위 큐에 저장한다.
앞선 내 풀이와 달라진 점은 큐에 해당 노드의 위치정보만 넣는 것이 아니라 cost까지 넣는다는 것이다.
그리고 방문할 수 있는 곳은 0으로, 방문할 수 없는 곳은 그차이로 cost를 설정해야 한다.
이때 우선순위 큐의 우선순위는 cost가 작은 노드이다.
2. 큐에서 데이터를 꺼내고 해당 노드가 아직 방문하지 않는 노드라면 방문처리한다. 이때 꺼낸 노드의 cost값을 전체 비용에 더해준다.
큐에서 나온 데이터는 cost가 제일 작은 노드이다. 해당 노드의 cost가 0이라면 방문할 수 있는 노드이고 0이 아니라면 방문할 수 없는 노드이다. 따라서 그때는 사다리를 놔야 하므로 cost값을 전체 비용에 더해줘야한다.
3. 1~2의 과정을 큐가 빌때까지 반복하면 된다.
이제 작성된 코드를 보자.
3. 코드
import java.util.Comparator;
import java.util.PriorityQueue;
public class Solution {
private static class Node {
int i, j, cost;
public Node(int i, int j, int cost) {
this.i = i;
this.j = j;
this.cost = cost;
}
}
public int solution(int[][] land, int height) {
int answer = 0;
int n = land.length;
// ❶ 주변 노드 탐색을 위한 di, dj
int[] di = {-1, 0, 1, 0};
int[] dj = {0, 1, 0, -1};
boolean[][] visited = new boolean[n][n];
// ❷ 시작 노드 추가
PriorityQueue<Node> pq = new PriorityQueue<>(Comparator.comparingInt(o -> o.cost));
pq.add(new Node(0, 0, 0));
// ❸ BFS + 우선순위 큐로 다음 노드 관리
while (!pq.isEmpty()) {
Node now = pq.poll();
// ❹ 아직 방문하지 않은 경로만 탐색
if (visited[now.i][now.j])
continue;
visited[now.i][now.j] = true;
// ❺ 현재까지 비용을 합산
answer += now.cost;
for (int i = 0; i < 4; i++) {
int ni = now.i + di[i];
int nj = now.j + dj[i];
// ❻ 유효한 인덱스가 아닐 경우
if (!(0 <= ni && ni < n && 0 <= nj && nj < n))
continue;
int tempCost = Math.abs(land[now.i][now.j] - land[ni][nj]);
// ❼ 입력으로 주어진 height 보다 높이차가 큰 경우
int newCost = tempCost > height ? tempCost : 0;
// ❽ 다음 경로를 add
pq.add(new Node(ni, nj, newCost));
}
}
return answer;
}
}출처: https://github.com/retrogemHK/codingtest_java/blob/main/solution/57.java
시간 복잡도
- O(N^2logN^2)
N: land의 한변의 길이.
각 지점을 방문하는데에 필요한 시간 복잡도는 O(N^2)이고 우선순위큐를 활용해 너비 우선탐색을 진행하므로 최종 시간복잡도는 O(N^2logN^2)이 된다.
'코딩 테스트 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 이진 변환 반복하기 (0) | 2024.06.23 |
|---|---|
| [프로그래머스] 전화번호 목록 (0) | 2024.06.21 |
| [프로그래머스] 튜플 (0) | 2024.06.20 |
| [프로그래머스] 가장 큰 수 (0) | 2024.06.20 |
| [프로그래머스] K번째 수 (0) | 2024.06.20 |
