1. 문제

프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
2. 풀이 과정

위와 같이 롤케잌의 각 조각의 토핑이 올려져있는 상황에서 롤케잌을 두 조각으로 나눌 때, 토핑의 종류를 동일하게 나누는 방법의 갯수를 세는 문제이다.
이 문제를 가장 쉽게 푼다면 나눌 수 있는 각 경우의 수에서 토핑의 종류를 각각 세서 같은지를 체크하는 식으로 풀 것이다..
하지만 이렇게 풀이하게 되면 시간복잡도가 O(N^2)이 되게 된다. 최대 토핑 배열의 길이가 100만이므로 O(N^2)으로는 해결할 수 없다.
따라서 나는 다음과 같은 방법으로 풀이했다.
롤케잌을 나눈 첫번째 조각의 토핑의 종류를 저장하는 해시셋이 p1, 두 번째 조각이 p2라고 할 때,
1. p2에 모든 롤케잌을 분배한다. 이때, p2에 분배하는 토핑의 종류별로 갯수를 세서 별도의 배열에 저장한다. 이 배열을 줄여서 개수 배열이라고 하겠다.
우선 토핑의 종류를 저장하기 위해서 중복 없이 종류만 셀때 사용하기 좋은 해시셋을 사용했다.
개수 배열을 생성한 이유는 아래서 설명하겠다.
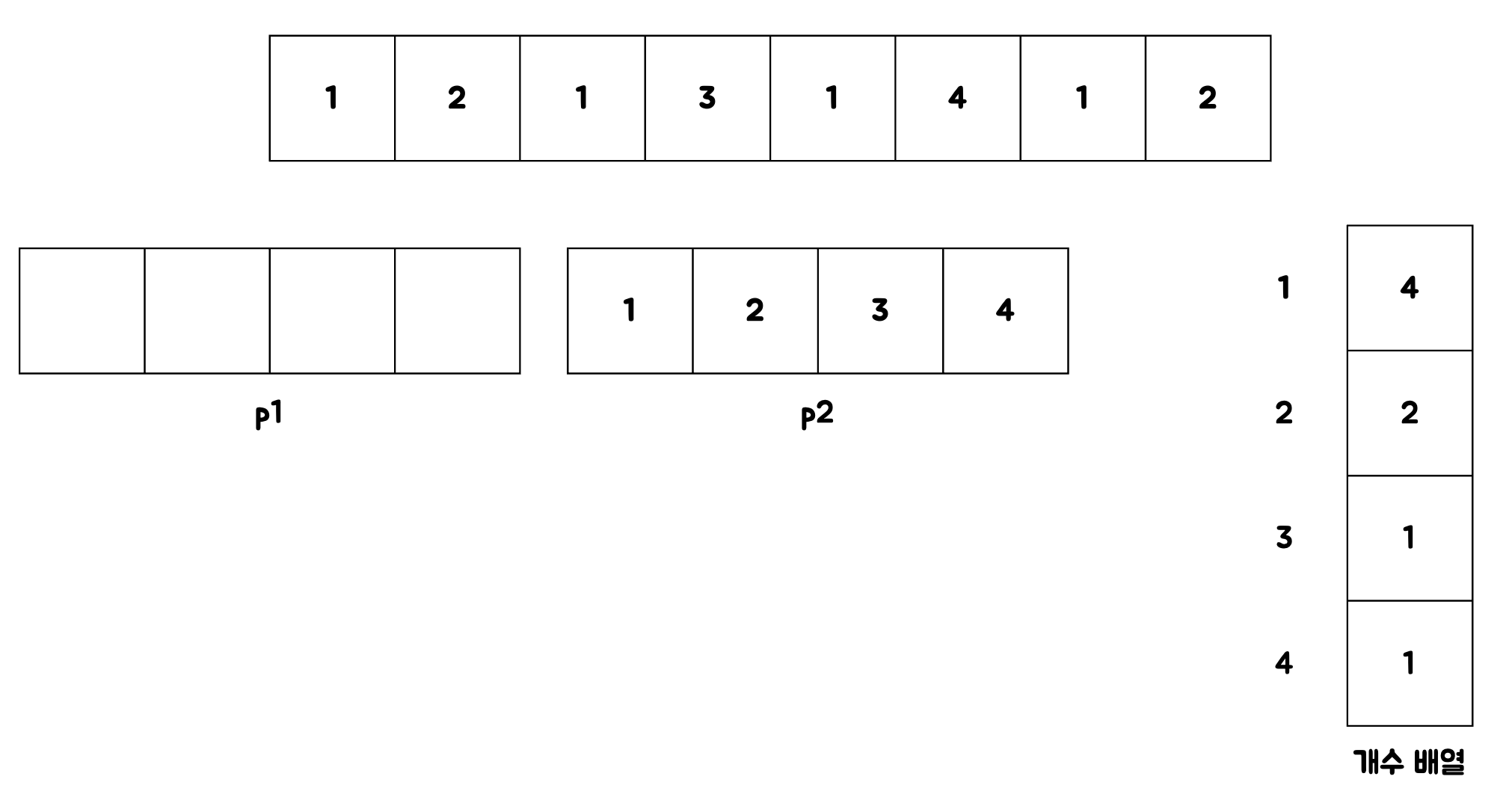
2. 롤케잌에 첫번째 조각부터 p1에 분배한다. 그리고 개수 배열에서 해당 조각의 토핑의 갯수를 하나 줄인다.
줄인후 해당 토핑의 갯수가 0이면 p2에 해당토핑을 제거한다.
제거 후의 p1과 p2의 길이가 같다면 공정하게 분배한 것이다.
개수 배열을 생성한 이유가 바로 여기서 나온다. 해당 토핑이 0이 되면 p2가 가지는 토핑의 종류는 하나 줄어든 것이다.
이를 통해 효율적으로 두 조각의 종류 수를 비교할 수 있다.
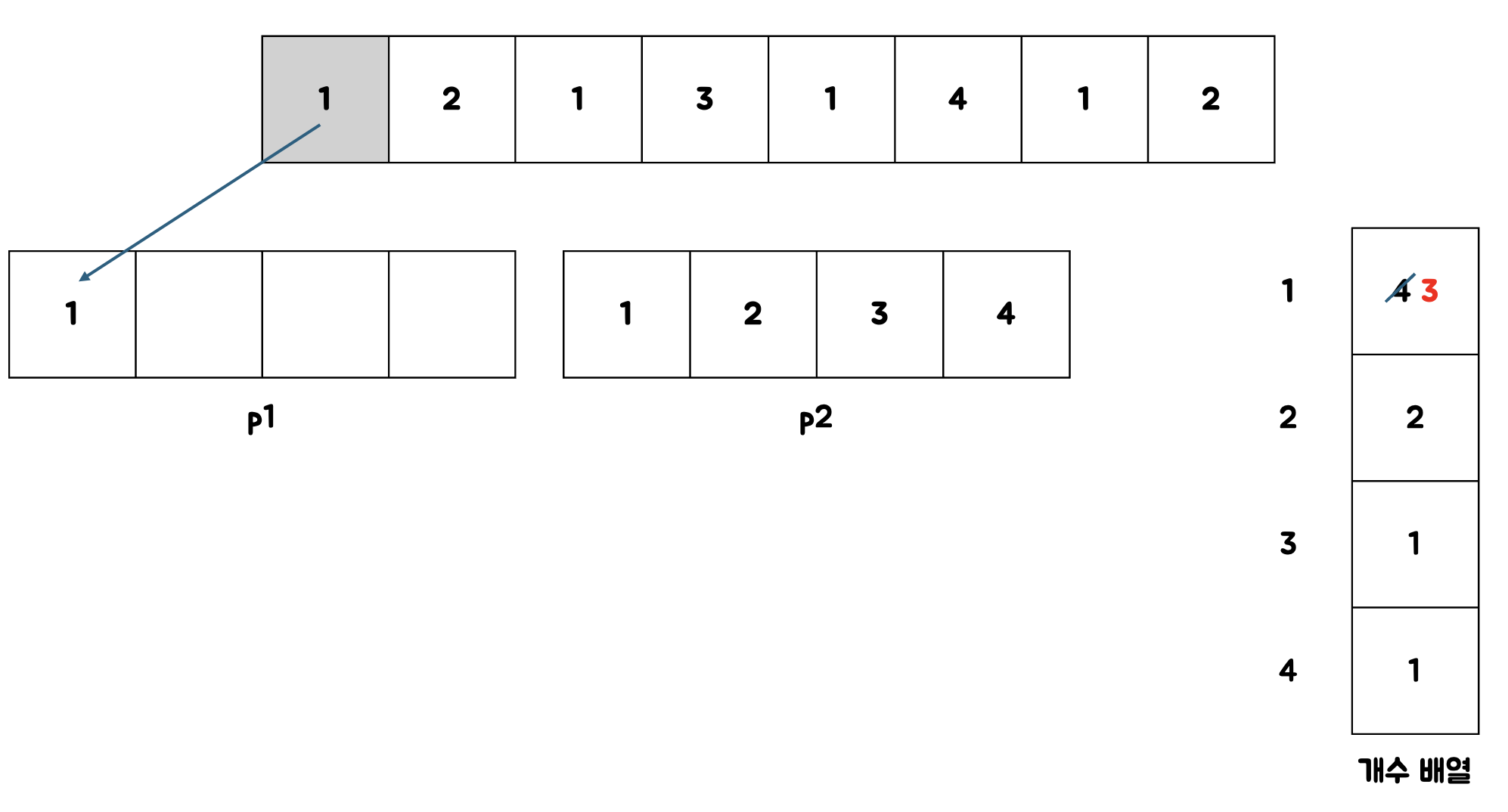

- 해당 케이스에서 토핑의 종류수가 3으로 같아지므로 공정하게 자른 것이다.
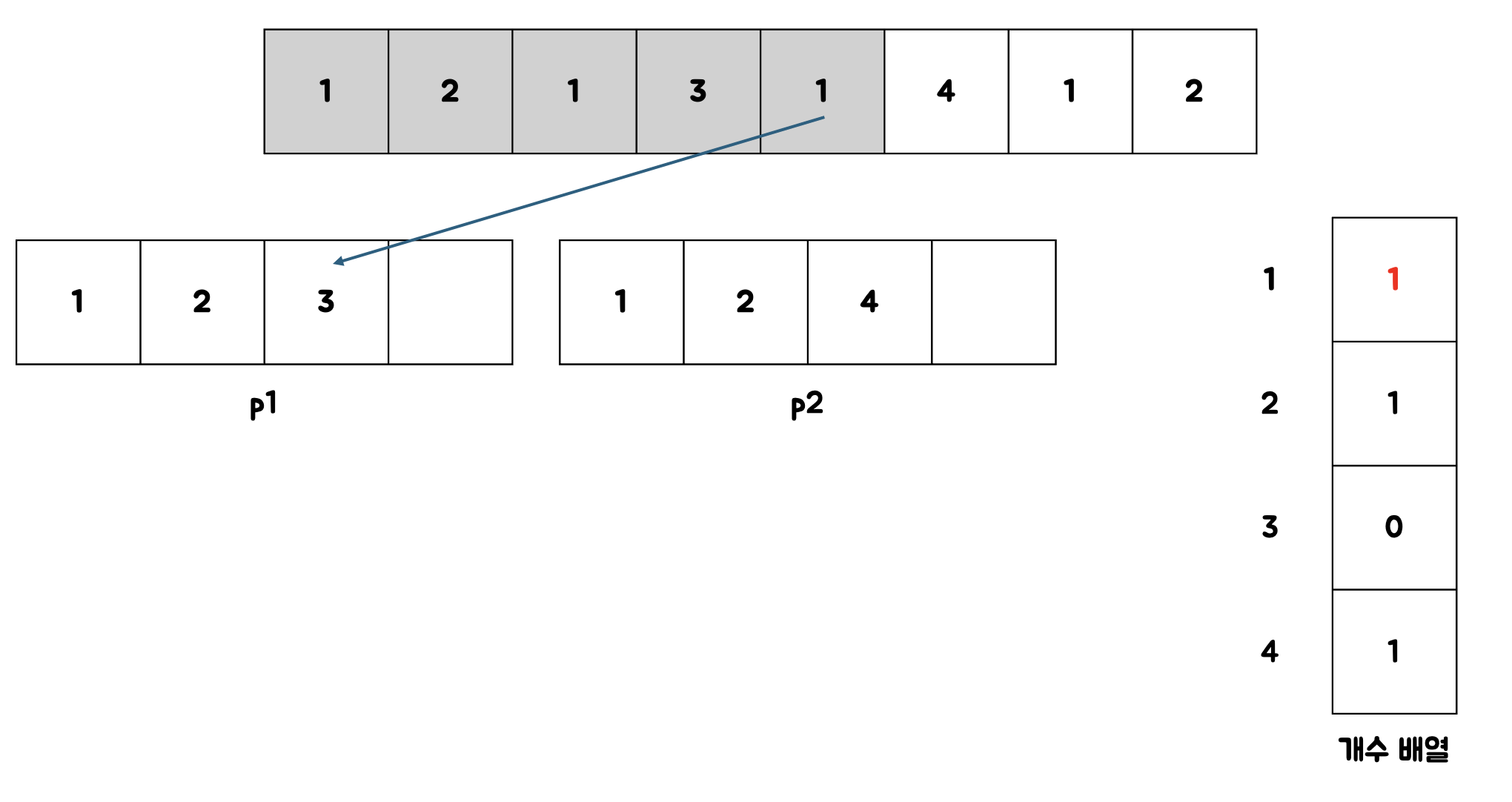
- 해당 케이스에서도 여전히 토핑의 종류 수가 3으로 같기 때문에 공정하게 자른 케이스가 하나 더 추가된다.
3. 내 코드
import java.util.*;
class Solution {
public int solution(int[] topping) {
Set<Integer> p1 = new HashSet<>();
Set<Integer> p2 = new HashSet<>();
int answer = 0;
int[] p2_count = new int[10001];
// p2에 모든 토핑을 저장하고 각 토핑의 갯수를 별도의 배열에 저장
for(int i = 0; i < topping.length; i++) {
p2.add(topping[i]);
p2_count[topping[i]]++;
}
for(int i = 0; i < topping.length; i++) {
// p1에 i번째 토핑 추가
p1.add(topping[i]);
// 갯수 배열에 해당 토핑 하나 제거
p2_count[topping[i]]--;
// 만약 해당 토핑의 남은 갯수가 0이라면 p2에서 해당 토핑 제거
if(p2_count[topping[i]] == 0)
p2.remove(topping[i]);
// p1과 p2의 크기가 같다면 answer +1
if(p1.size() == p2.size())
answer++;
}
return answer;
}
}시간 복잡도
- O(N)
'코딩 테스트 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 점프와 순간 이동 (0) | 2024.06.23 |
|---|---|
| [프로그래머스] 카펫 (0) | 2024.06.23 |
| [프로그래머스] 이진 변환 반복하기 (0) | 2024.06.23 |
| [프로그래머스] 전화번호 목록 (0) | 2024.06.21 |
| [프로그래머스] 지형 이동 (0) | 2024.06.21 |
