동적 계획법(Dynamic Programming)이란?
동적 계획법이란 전체 문제를 한 번에 해결하는 것이 아니라 작은 부분 문제들을 해결하고 이를 활용하여 전체 문제를 해결하는 방법이다.
하지만 동적 계획법은 작은 부분 문제들을 통해 전체 문제를 해결한다고 해도 반드시 효율적인 것은 아니다.
동적 계획법을 효율적으로 사용하기 위해선 다음의 두 가지 조건을 만족해야 한다.
1. 큰 문제를 작은 문제로 나누었을 때 동일한 작은 문제가 반복적으로 등장해야 한다.
2. 큰 문제의 해결책은 작은 문제의 해결책의 합으로 구할 수 있어야 한다.
어떠한 문제를 다음과 같이 작은 문제로 나누었다고 해보자.
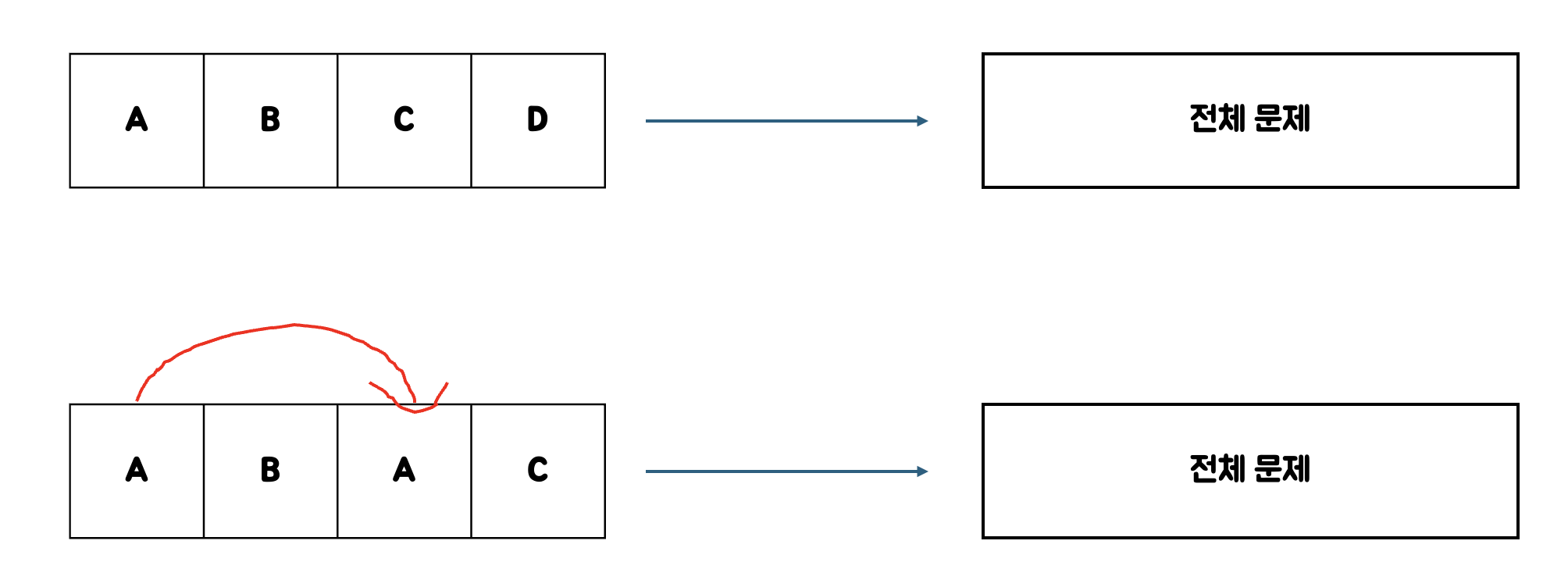
- A, B, C, D의 작은 문제로 하나의 전체 문제를 푼다고 했을 때, 이 경우는 동일한 작은 문제가 반복적으로 등장하지 않는다. 따라서 동적 계획법을 사용하기 효율적인 케이스는 아니다.
- A, B, A, C의 작은 문제로 하나의 전체 문제를 푼다고 했을 때, 이 경우는 A가 반복해서 등장한다. 이 경우 이전에 풀었던 A를 활용해 다음 A를 풀 때 활용할 수 있다.
이러한 동적계획법의 대표적인 문제가 피보나치 수열이다.
피보나치 수열은 다음과 같이 큰 문제를 작은 문제로 나눌 수 있고 동일한 작은 문제가 여러번 등장한다.

지금부터 피보나치 수열을 통해 동적계획법을 자세히 설명해보겠다.
동적 계획법 해결 절차
동적 계획법을 해결하는 절차는 다음과 같다.
1️⃣ 문제를 해결하는 해가 이미 있다고 가정한다.
2️⃣ 종료 조건을 설정한다.
3️⃣ 과정 1, 2를 활용해 점화식을 세운다.
이제 피보나치 수열을 위와 같은 절차로 풀어보자.
1️⃣ 문제를 해결하는 해가 이미 있다고 가정한다.
피보나치 수열을 해결하는 어떠한 함수 fibo(n)이 있다고 가정해보자.
2️⃣ 종료 조건을 설정한다.

fibo(n)은 위와 같이 n번째 해가 n-1과 n-2번째 해의 합이 된다.
단, n이 1 또는 2일때는 1이 해가 된다.따라서 fibo(n)의 종료조건은 n=1 또는 n=2가 된다.
3️⃣ 과정 1, 2를 활용해 점화식을 세운다.
fibo(n)의 점화식은 다음과 같다.
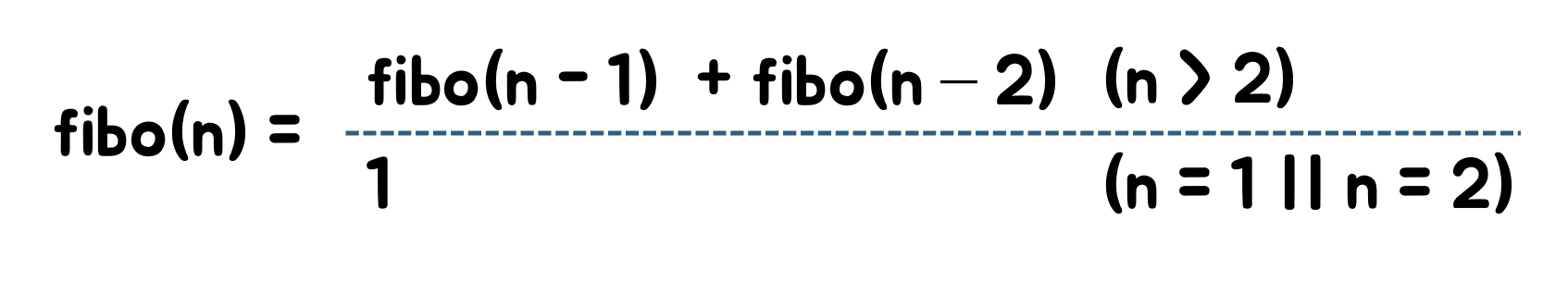
동적 계획법 구현 패턴
앞에서 설명했듯, 동적 계획법의 핵심은 점화식이다. 따라서 이 점화식을 구현하는 것이 동적계획법의 핵심이라고 할 수 있다.
점화식은 보통 재귀를 통해 구현할 수 있다.
피보나치 수열을 재귀를 통해 구현하면 다음과 같을 것이다.
int fibo(n) {
if(n == 1 || n == 2)
return 1; // 종료 조건
else
return fibo(n-1) + fibo(n-2);
}
메모이제이션(Memoization)
fibo(n)의 함수호출스택에 쌓이는 순서는 다음과 같다.
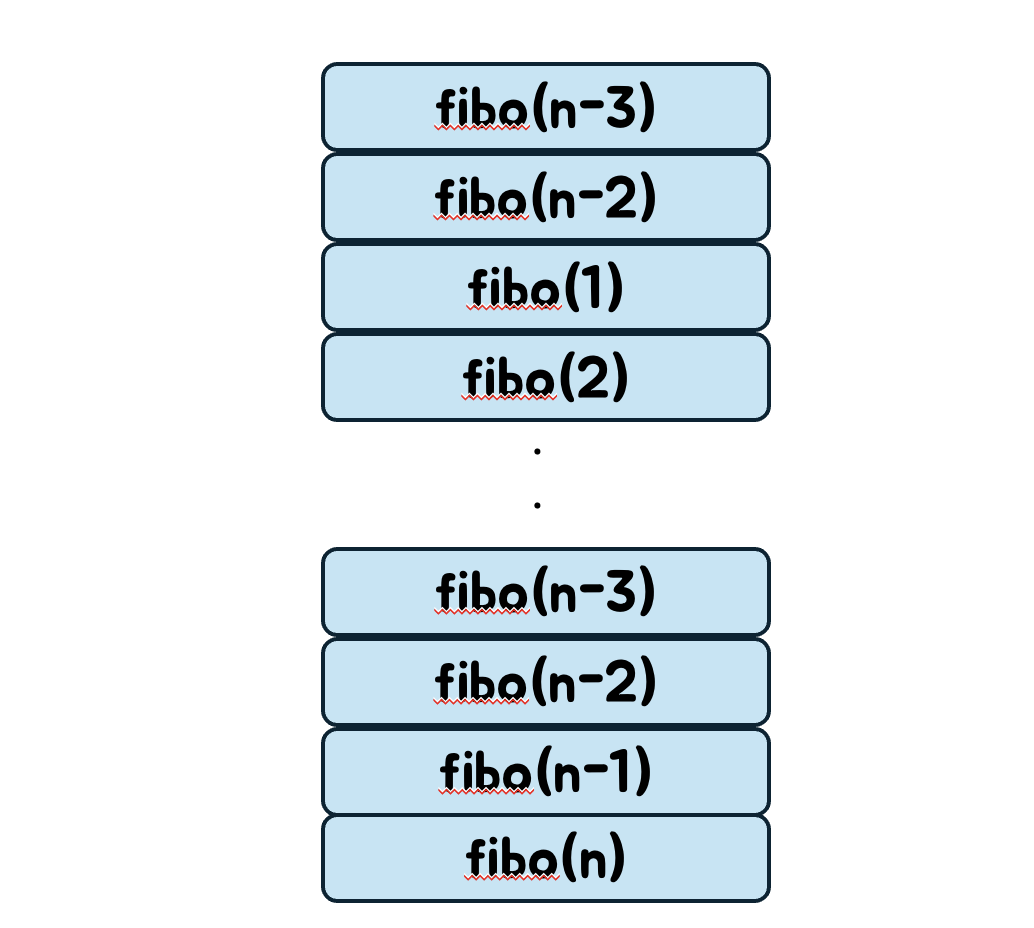
보면 같은 값이 여러 번 반복해서 등장하는 것을 알 수 있다.
이러한 특성때문에 n이 매우커지게 되면 함수스택에 오버플로우가 발생할 수 있다.
이 문제를 해결하는 것이 메모이제이션이다.
메모이제이션이란, 이미 계산한 값을 저장해두었다가 이후 쓸 일이 있을 때 활용하는 것을 의미한다.
메모이제이션은 흔히 배열을 통해 구현한다.
피보나치 수열에서 메모이제이션을 사용하는 방법은 다음과 같다.
예를 들어, fibo(5)를 구한다고 해보자.
재귀적으로 호출하다보면 fibo(3)이 종료조건인 fibo(2)와 fibo(1)을 호출하게 된다.

이때부터 메모이제이션이 시작된다.
fibo(1)과 fibo(2)의 값인 1을 배열에 저장한다.
fibo(3)은 메모이제이션된 값을 통해 구할 수 있다.
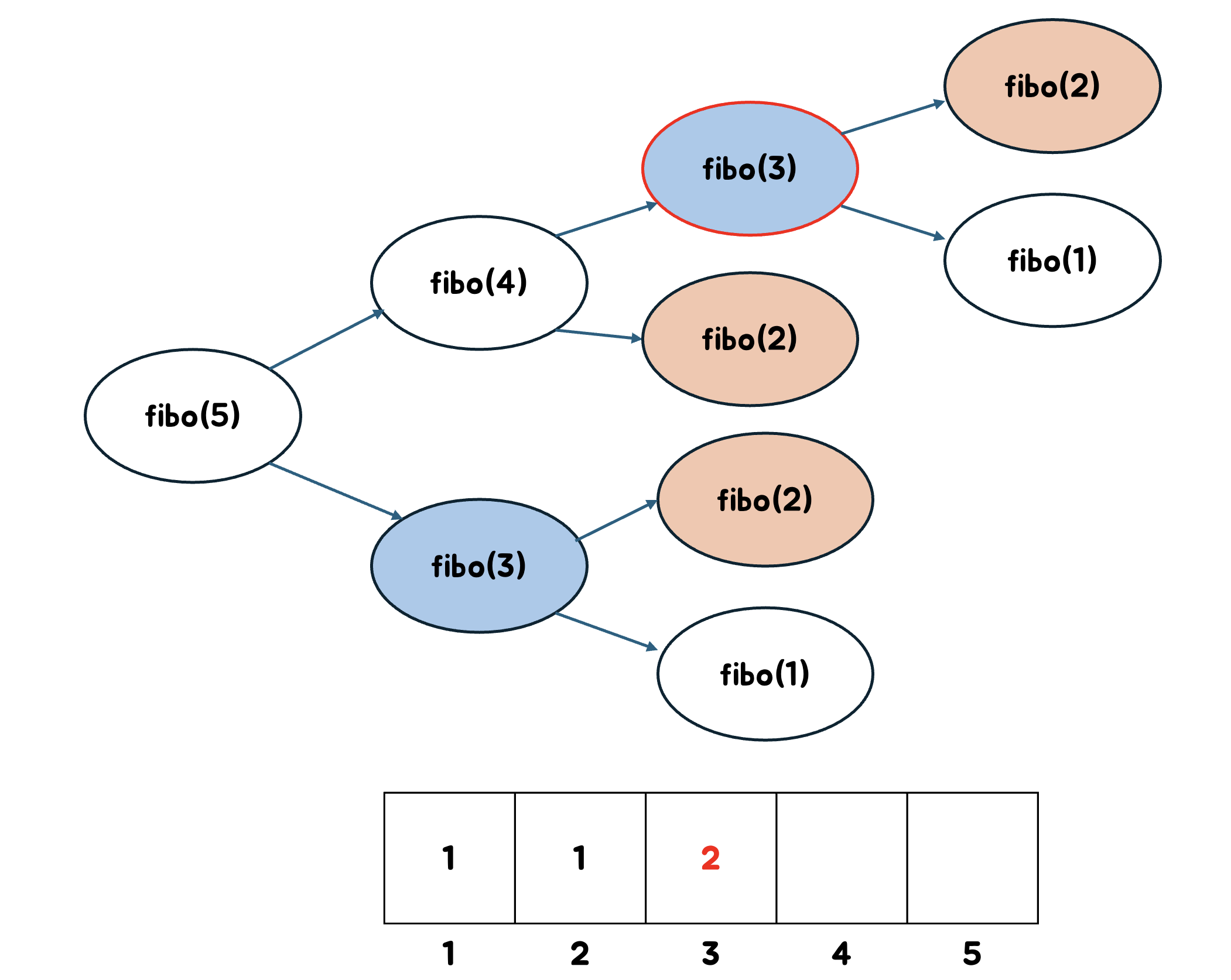
메모이제이션 된 fibo(1)과 fibo(2)의 값을 통해 fibo(3)의 값을 알 수 있다.
fibo(4)도 마찬가지이다.

메모이제이션된 fibo(3)과 fibo(2)를 통해 알 수 있다.
최종적인 답, fibo(5)를 보면 메모이제이션의 장점이 확 체감될 것이다.
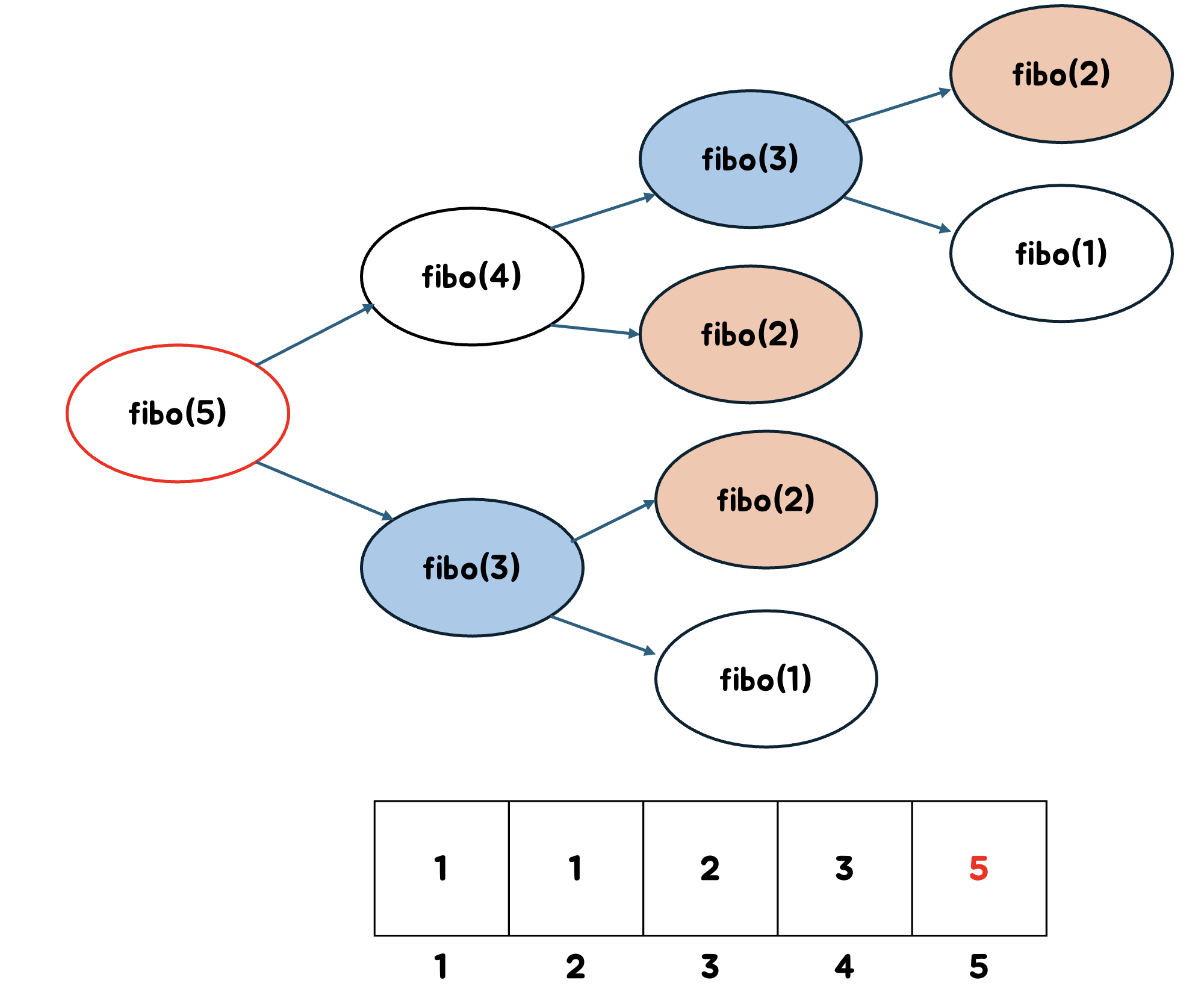
원래대로라면, fibo(4)와 fibo(3)을 구하기 위해 반복적으로 재귀호출 해야했다.
하지만 해당 값이 메모이제이션이 돼있다면 재귀호출할 필요 없이 그냥 그 값을 반환하기만 하면된다.
메모이제이션을 활용한 피보나치 수열을 구현해보면 다음과 같다.
int[] fibo_data;
public int fibo(int n) {
// 해당 값이 메모이제이션 돼있다면 해당 값을 배열에서 반환
if(fibo_data[n] != 0) return fibo_data[n];
// 종료조건 메모이제이션
if(n == 1 || n == 2) {
fibo_data[n] = 1;
return 1;
}
// 그 외 메모이제이션
else {
fibo_data[n] = fibo(n - 1) + fibo(n - 2);
return fibo_data[n];
}
}
동적 계획법 대표문제
최장 증가 부분 수열(LIS - Longest Increased Subsequence)
부분 수열이란?
LIS를 이해하기 위해서는 부분 수열의 개념을 이해해야한다.
부분 수열이란 주어진 수열 중 일부를 뽑아 새로 만든 수열을 의미한다.
수열이기 때문에 당연히 순서는 유지된다.
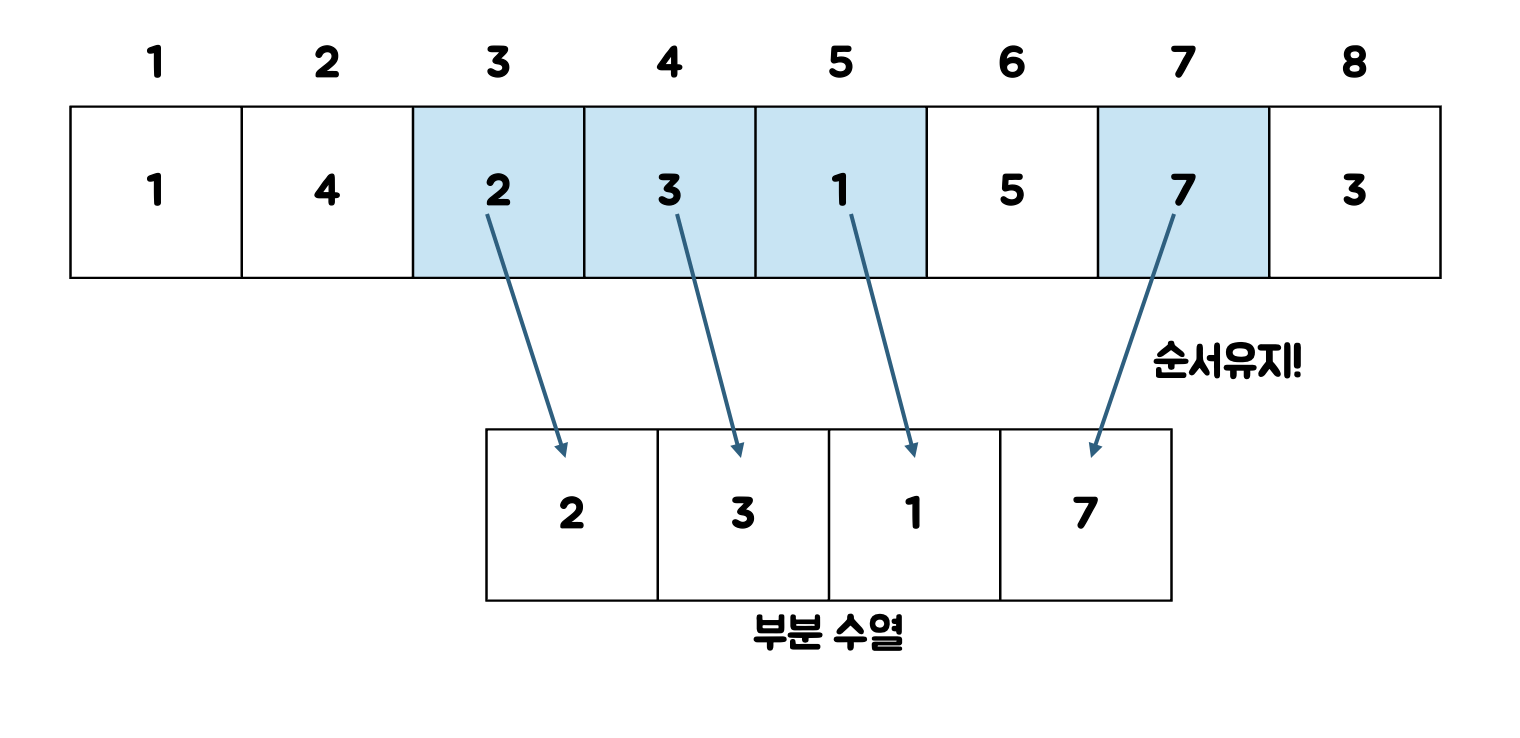
최장 증가 부분 수열(LIS)란?
LIS는 오름차순으로 증가하는 부분 수열 중 길이가 가장 큰 부분 수열을 말한다.

❗️주의: LIS는 엄격하게 오름차순이어야 한다. 예를 들어 부분 수열이 [1, 1, 3, 5]라면 LIS가 아니다.
LIS의 길이를 동적 계획법으로 구하기
이제 동적 계획법으로 LIS의 길이를 구해보자.
LIS를 작은 문제로 쪼개면 다음과 같다.
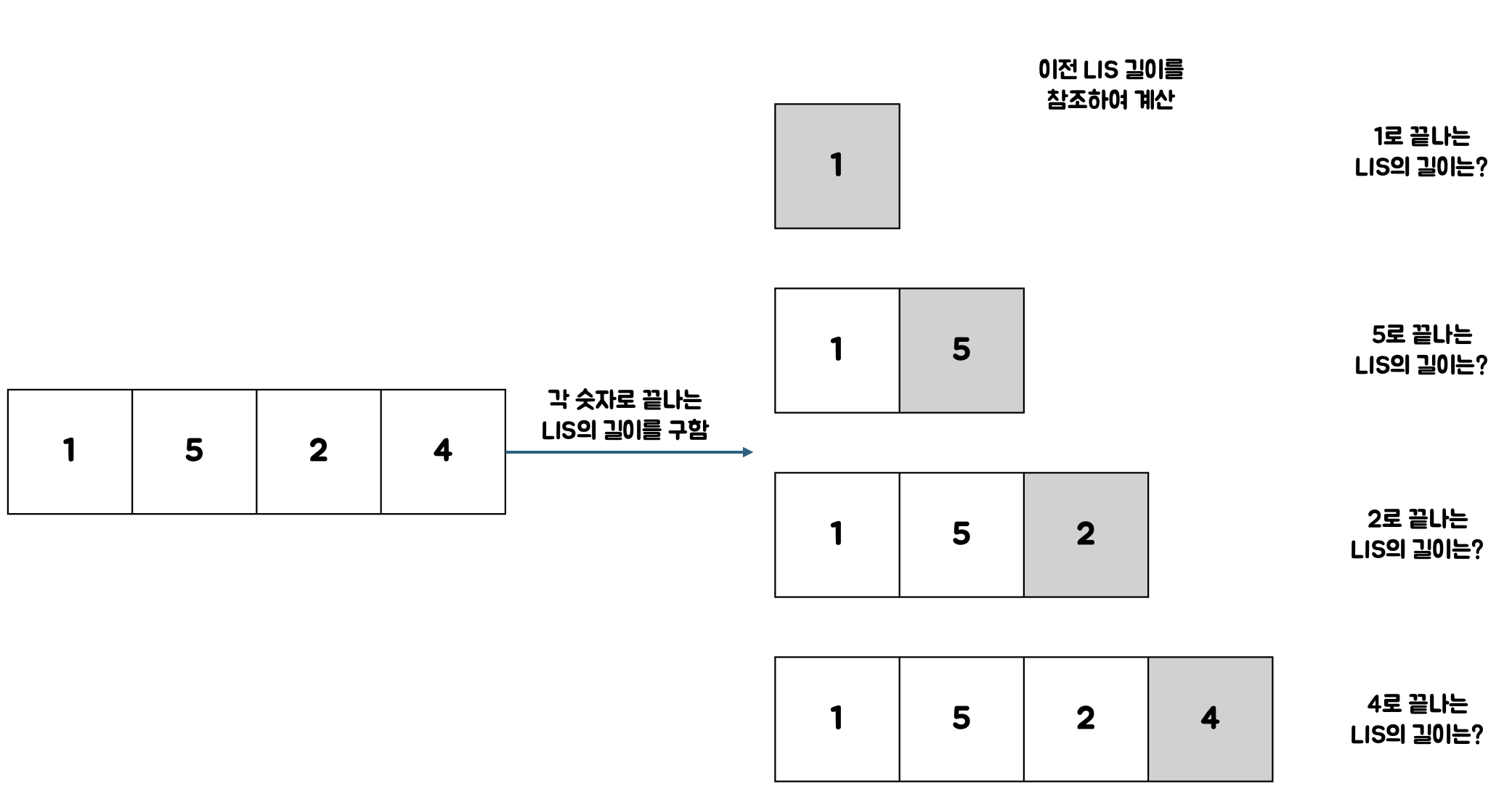
전체 LIS의 길이를 구하는 문제는 각 숫자로 끝나는 LIS의 길이 중 가장 큰 LIS의 길이를 구하는 문제로 바꿀 수 있다.
이때 각 숫자의 LIS는 이전 숫자들의 LIS 길이를 참조하여 계산된다.
5의 경우 1로 끝나는 LIS 길이를 참조하고
2의 경우 1, 5로 끝나는 LIS 길이를 참조하고
4의 경우 1, 5, 2로 끝나는 LIS 길이를 참조한다.
그렇다면 현재 숫자로 끝나는 LIS 길이는 어떻게 구할까?
다음과 같은 수열이 있다고 해보자.

첫 번째 숫자의 경우 LIS의 길이는 무조건 1이다.

두 번째 숫자의 경우 첫 번째 숫자인 1보다 크기 때문에 [1, 4]가 LIS가 된다. 따라서 LIS길이는 2가 된다.

세 번째 숫자의 경우 두 번째 숫자인 4보다는 작지만 첫 번째 숫자인 1보다 크기 때문에 [1, 2]가 LIS가 된다.
따라서 LIS 길이는 2이다.

네 번째 숫자의 경우 두 번째 숫자인 4보다는 작지만 첫 번째, 세 번째 숫자인 1과 2보다는 크기 때문에 [1, 2, 3]이 LIS가 된다.
따라서 LIS 길이는 3이다.
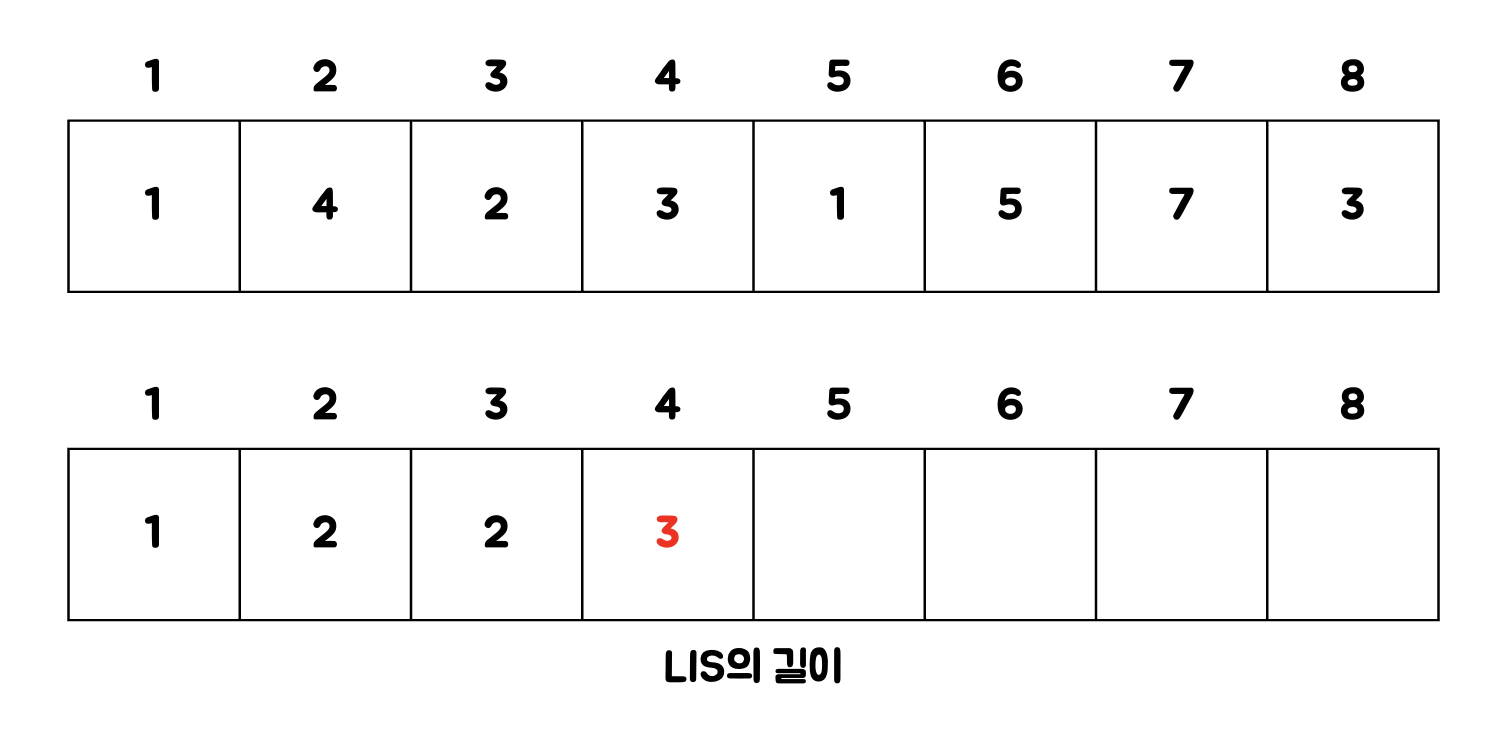
다섯 번째 숫자의 경우 모든 이전 숫자보다 크지 않다. 이 경우 [1]이 LIS가 된다.
따라서 LIS 길이는 1이다.
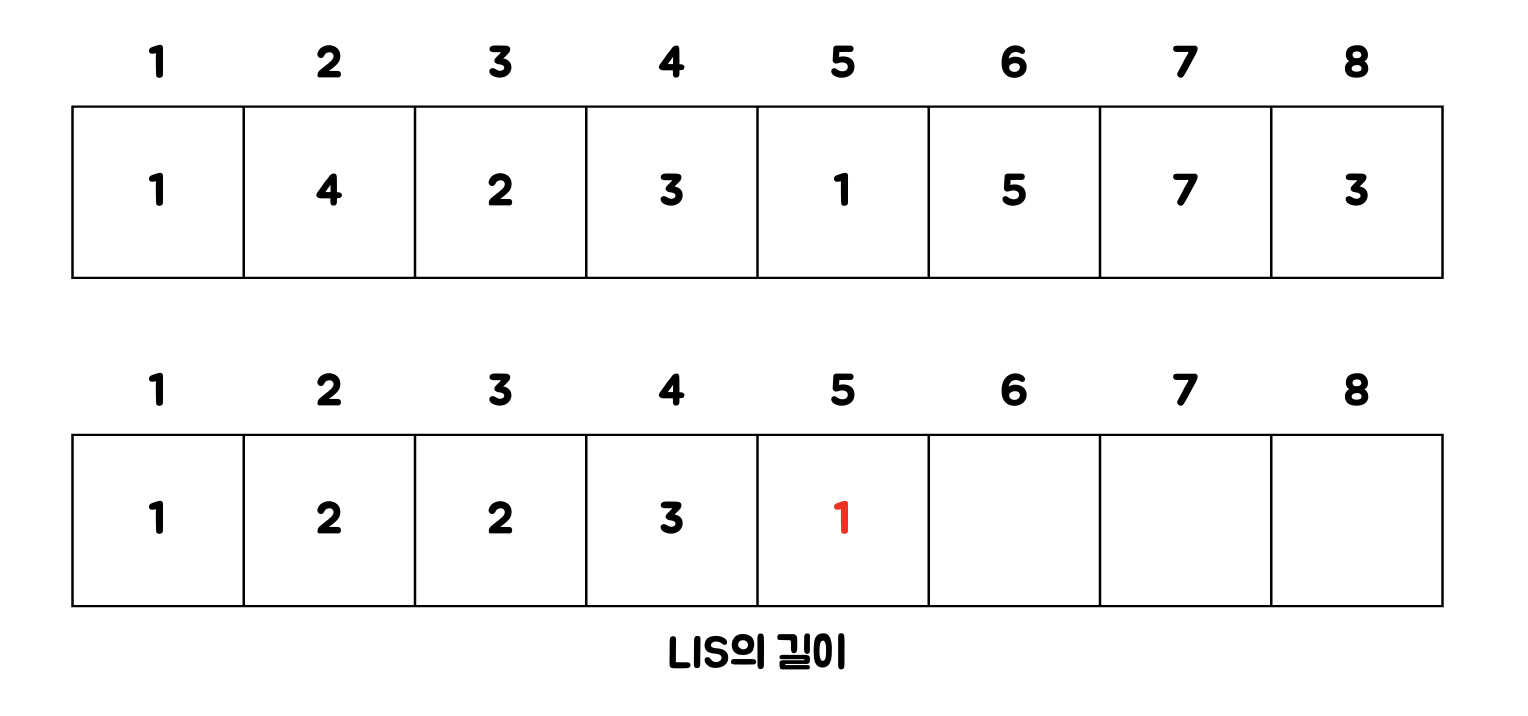
이를 반복하면 최종 결과는 다음과 같다.

7로 끝나는 LIS가 5로 가장 크기 때문에 최종적인 답은 5가 된다.
지금까지의 과정을 보면, 약간의 패턴이 보인다.
N번째 숫자로 끝나는 LIS의 길이는 이전 숫자중 N보다 크지 않은 숫자의 LIS 길이 중 최댓값에 1을 더한 것이다.
이를 통해 다음과 같은 점화식을 세울 수 있다.

이렇게 해서 모든 N에 대해 LIS_LEN을 구하고 LIS_LEN(N) 중 최댓값이 최종 정답이 된다.
구현(자바)
private static int[] lis;
private static int LIS(int[] nums) {
// 1️⃣ lis[i]는 nums[i]를 마지막으로 하는 LIS의 길이를 저장하는 배열
lis = new int[nums.length];
// 2️⃣ 첫번째 값을 마지막으로하는 LIS의 길이는 항상 1
lis[0] = 1;
// 3️⃣ 동적 프로그래밍을 통해 LIS 계산
for (int i = 1; i < lis.length; i++) {
// 4️⃣nums[i]보다 작은 값 중에서 최댓값 찾기
int max = Integer.MIN_VALUE;
for (int j = i - 1; j >= 0; j--) {
if (nums[i] > nums[j] && nums[j] > max)
max = nums[j];
}
lis[i] = max;
}
// 5️⃣ LIS 값 중 최댓값 반환
return Arrays.stream(lis).max().getAsInt();
}
최장 공통 부분 수열(LCS - Longest Common Subsequence)
최장 공통 부분 수열(LCS)란?
최장 공통 부분 수열(LCS)이란, 두 수열이 있을 때, 각각의 부분 수열 중에서 구성 원소가 공통되면서 길이가 가장 큰 부분 수열을 의미한다.
이때 수열은 꼭 숫자로 이루어지지 않아도 된다. 어떠한 객체의 형태도 상관없다.
보통 LCS는 문자열의 공통 부분 집합을 찾을 때 많이 사용된다.
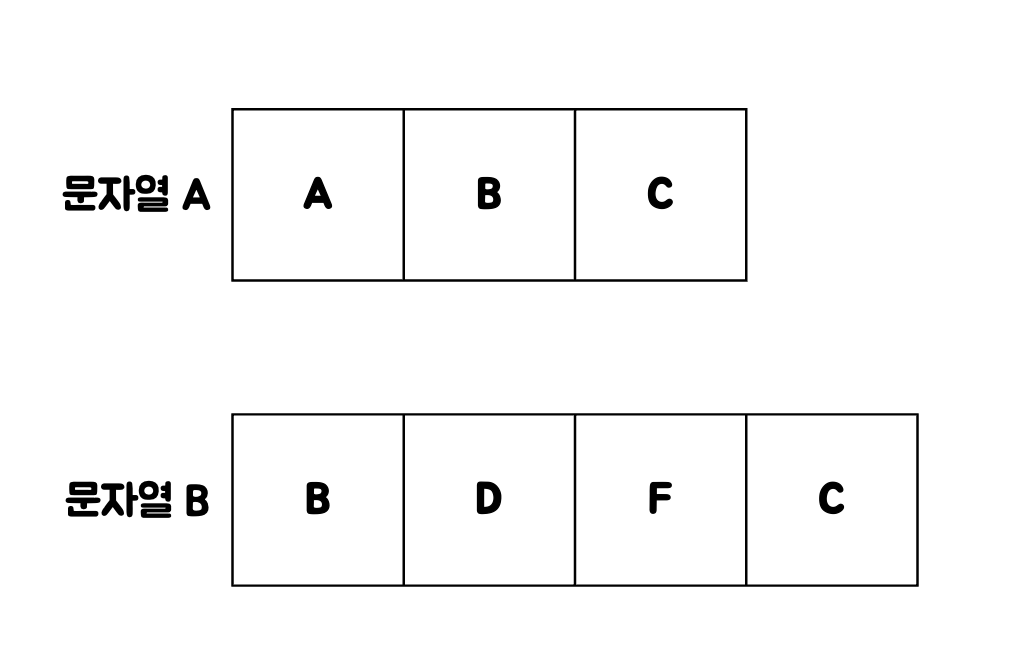
두 문자열 A, B의 LCS는 다음과 같다.

LCS의 길이 동적 계획법으로 구현하기
일단 문제를 작은 문제로 나누어 보자.
1️⃣ 두 문자열의 길이가 1인 경우를 생각해보자.
이 경우는 간단하다. 두 문자열의 같으면 LCS가 1이고 아니면 0이다.
2️⃣ 조금 더 긴 문자열
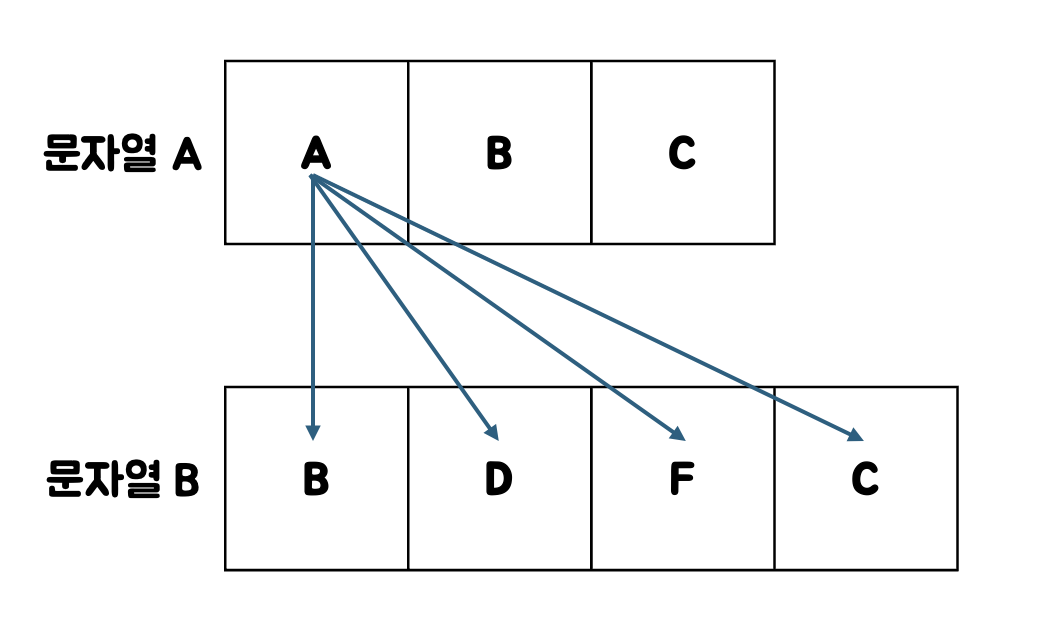
1. 문자열 A의 첫 번째 ~ 마지막 문자를 문자열 B의 문자와 하나식 짚어가며 같은 것이 있는지 확인한다.
2. A[1]과 B의 문자와 같은 경우가 없으므로 넘어간다.
3. A[2]의 경우 B[1]의 문자와 'B'로 같고 또 A[3]의 경우 B[4]의 문자와 'C'로 같다.
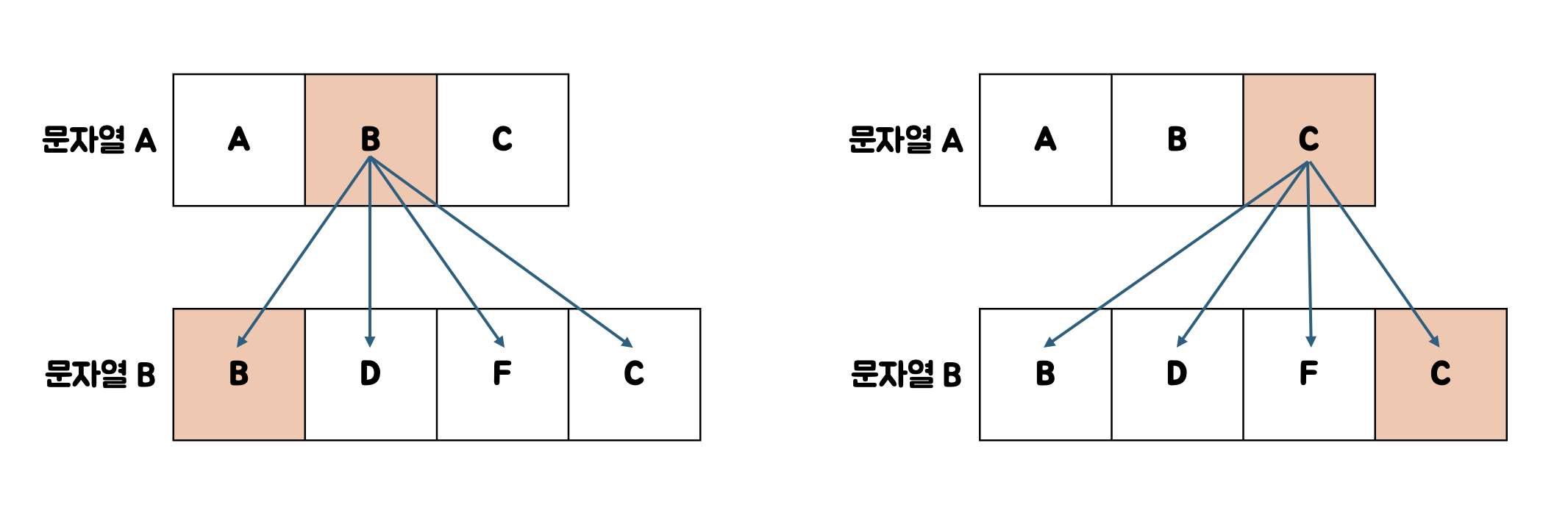
이 경우, LCS는 'BC'가 된다.
하지만 주의해야할 것이 있다.
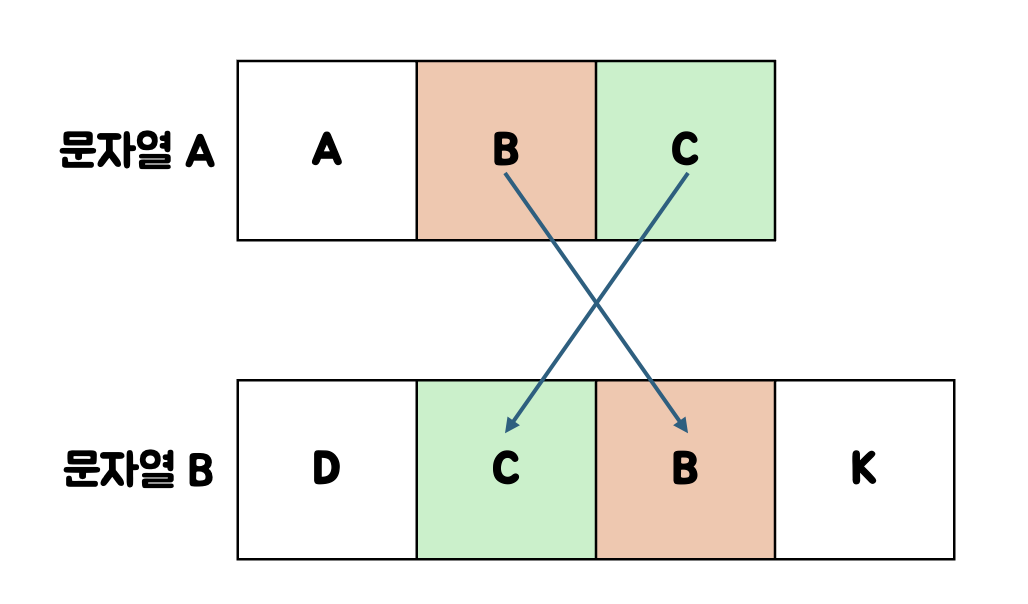
위와 같이 문자의 순서가 역방향이라면 LCS가 될 수 없다.
이 점을 잘 기억하며 LCS의 길이를 찾는 점화식을 생각해보자.
LCS의 길이 점화식
첫번째 문자열의 1번째 부터 i번째 문자열과 두 번째 문자열의 1번째 부터 j번째 문자열 간의 LCS의 길이를 LCS(i, j)라고 해보자.
앞서 말했듯 두 문자열의 길이가 모두 1일 때, 문자가 같다면 1, 다르면 0이다. 즉, LCS(1, 1) = 1 or 0
여기서 문자를 하나씩 확장 시켜서 LCS(2, 2)를 구하는 경우를 생각해보자.

- 2번째 문자가 서로 같으면 LCS(2, 2)는 LCS(1, 1)에 + 1을 한 값이다.
- 2번째 문자가 서로 다르면 LCS(2, 2)는 다음 두 가지 값 중 큰 값이다.
- ❶ LCS(1, 2)
- ❷ LCS(2, 1)
두 문자가 같은 경우는 이해가는데 다른 경우가 이해가 잘 안간다.
더 자세한 예시를 통해 생각해보자.
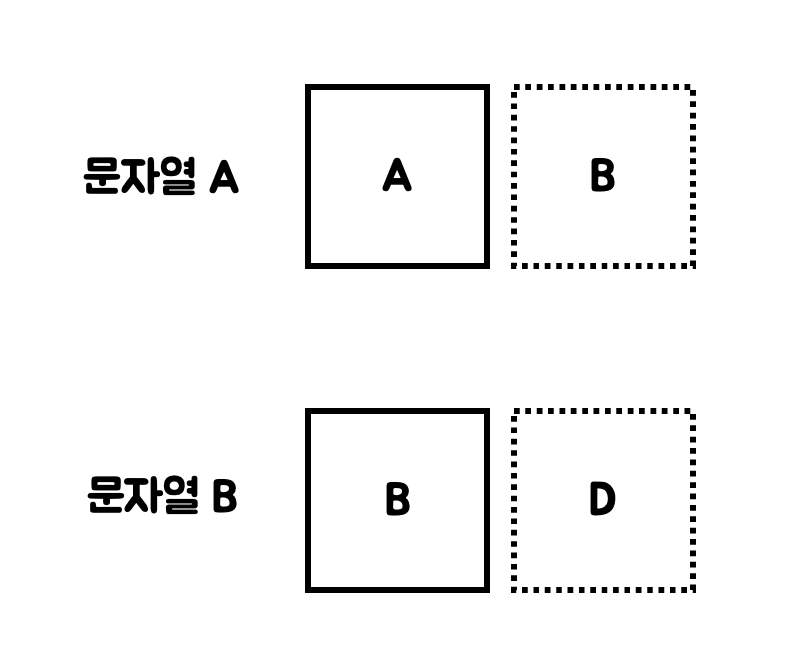
위의 예시에서 두 번째 문자열은 서로 다르다. 따라서 이 경우 LCS(2, 2)를 LCS(1, 2)와 LCS(2, 1) 중 최댓값으로 해야한다.
- LCS(1 ,2)의 경우 A와 D가 같지 않기 때문에 LCS(1, 1) 또는 LCS(0, 2)를 봐야한다. 둘 다 0이므로 LCS(1, 2)는 0이다.
- LCS(2, 1)의 경우 B와 B가 같다. 따라서 LCS(2, 1)은 1이다.
그렇기 때문에 최종적인 LCS(2, 2)는 1이 된다.
이를 통해 LCS(i, j)에 대해 점화식을 작성하면 다음과 같다.

LCS(i, j)의 최댓값이 최종 정답이 된다.
구현 (자바)
int LCS(String str1, String str2) {
// 1️⃣ 두 문자열의 길이를 저장
int m = str1.length();
int n = str2.length();
// 2️⃣LCS를 저장할 테이블 초기화
dp = new int[m + 1][n + 1];
// 3️⃣동적 프로그래밍을 통해 LCS 길이 계산
for(int i = 1; i <= m; i++) {
for(int j = 1; j <= n; j++) {
char str1_c = str1.charAt(i - 1);
char str2_c = str2.charAt(j - 1);
// 4️⃣현재 비교하는 문자가 같으면
if(str1_c == str2_c)
dp[i][j] = dp[i - 1][j - 1] + 1;
// 5️⃣현재 비교하는 문자가 다르면
else
dp[i][j] = Integer.max(dp[i - 1][j], dp[i][j - 1]);
}
}
// 6️⃣LCS 길이 반환
return dp[m][n];
}
여기서 한 가지 지켜봐야할게 맨 마지막 부분이다.
return dp[m][n];위에서 설명할 때 dp 배열의 최댓값이 정답이라고 했는데 여기선 마지막 인덱스 값을 반환했는데
조금만 생각해보면 마지막 인덱스 값에는 항상 dp 배열의 최댓값이 들어간다는 것을 알 수 있다.
'코딩 테스트 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 그리디(Greedy) 알고리즘 (0) | 2024.06.25 |
|---|---|
| 행렬의 연산 (0) | 2024.06.22 |
| 정렬(Sort) (0) | 2024.06.19 |
| 백트래킹(BackTracking) 알고리즘 (0) | 2024.06.13 |
| 그래프 최단 경로 알고리즘 - 벨만 포드(Bellman-Ford) 알고리즘 (2) | 2024.05.31 |
