그리디 (Greedy) 알고리즘이란?
그리디(Greedy)는 사전적으로 '탐욕적인'이라는 뜻이다.
그리디 알고리즘은 말 그대로 탐욕적인 알고리즘이다.
그리디 알고리즘은 현재 상황에서 가장 최적의 해를 선택을 하며 선택을 번복하지 않는다.
이러한 특성을 가지고 지역 최적해를 추구한다고 이야기 하기도 한다.
이렇게 선택을 반복해 하나의 문제를 푸는 알고리즘이다.
하지만 그리디 알고리즘을 모든 상황에서 적용가능한 것은 아니다.
현재 상황의 최적의 해가 전체 상황의 최적의 해를 보장하는 것은 아니기 때문이다.
그렇다면 해당 문제가 그리디 알고리즘으로 해결이 가능한지 어떻게 알 수 있을까?
그리디 알고리즘으로 문제를 해결하기 위해선 다음의 두 가지 조건을 만족해야한다.
1. 최적 부분 구조: 부분해를 구하는 과정이 최적해를 구하는 과정과 일치
2. 그리디 선택 속성: 선택 과정이 다른 과정에 영향을 주지 않음
그럼 지금부터 그리디 알고리즘의 대표문제들을 통해 더 자세히 이해해보자.
잔돈 문제
잔돈 문제는 대표적인 그리디 알고리즘 문제이다.
여러 종류의 동전이 있을 때, 특정 금액의 거슬러를 주기 위한 최소한의 동전을 사용하는 방법을 알아내는 문제이다.
이 문제는 그리디 문제일 수도 있고 아닐 수도 있다.
예시를 통해 그 이유를 설명해보겠다.
그리디 알고리즘으로 풀 수 있는 경우
예를 들어 동전 단위가 10, 50, 100, 500이 있다고 해보자. 동전의 갯수는 충분히 있다.
이때 1260원을 거슬러 준다고 할 때, 이를 그리디 알고리즘으로 접근해보자.
최소 갯수의 동전으로 거슬러를 주기 위해선 가장 큰 단위의 동전부터 줘야 한다.
즉, 현재 상황에서 최적의 해는 거슬러 금액을 넘지 않는 단위가 가장 큰 동전이다.
1. 500원으로 거슬러 (1260원)
최대 2개까지 선택할 수 있다.
그결과 260원이 남는다.
2. 100원으로 거슬러 (260원)
최대 2개까지 선택할 수 있다.
그 결과 60원이 남는다.
3. 50원으로 거슬러 (60원)
1개까지 선택할 수 있다.
그 결과 10원이 남는다.
4. 10원으로 거슬러 (10원)
1개까지 선택할 수 있다.
남은 금액이 없으므로 모든 거슬러를 줬다.
따라서 500원 2개, 100원 2개, 50원 1개, 10원 1개 총 6개의 동전으로 주는 것이 최소 갯수의 동전으로 거슬러를 주는 방법이다.
하지만 같은 문제여도 특정 상황에선 그리디 알고리즘으로 풀 수 없다.
다음 경우를 보자.
그리디 알고리즘으로 풀 수 없는 경우
동전단위가 1, 3, 4가 있고 6원을 거슬러 주는 경우를 생각해보자.
똑같이 그리디적으로 접근해보자.
1. 4원으로 거슬러(6원)
최대 1개까지 선택할 수 있다.
그 결과 2원이 남는다.
2. 3원으로 거슬러(2원)
남은 돈이 2원이기 때문에 3원으로는 거슬러를 줄 수가 없다.
3. 1원으로 거슬러(1원)
최대 2개까지 선택할 수 있다.
남은 금액이 없으므로 모두 거슬러 줬다.
그리디로 풀었을 때, 답은 4원 1개, 1원 2개 총 3개가 정답이 된다.
하지만 이것이 진짜로 정답일까? 아니다. 바로 3원짜리를 2개 주면 2개로도 거슬러를 줄 수 있다.
따라서 그리디 알고리즘이 모든 상황에서 적용이 가능했던 것은 아니다.
그렇다면 동전 문제에서 그리디로 해결 가능한 경우는 어떤 경우이고 해결 불가능한 경우는 어떤 경우일까?
동전 문제 그리디 해결 조건
동전 문제를 그리디로 해결하려면 동전들의 관계가 모두 배수 관계 이어야 한다.
1, 50, 100, 500의 경우 서로 모두 배수 관계이었기 때문에 현재 동전의 해가 다른 동전의 해에 영향을 미치지 않는다.
반면 1, 3, 4의 경우 배수 관계가 아니다. 따라서 앞선 동전의 해가 다른 동전의 해에 영향을 미친다.
앞서 그리디 알고리즘으로 문제를 해결하기 위해선 다음의 두 가지 조건을 만족해야 한다고 했다.
1. 최적 부분 구조: 부분해를 구하는 과정이 최적해를 구하는 과정과 일치
2. 그리디 선택 속성: 선택 과정이 다른 과정에 영향을 주지 않음
동전 문제는 현재의 동전이 서로 배수일 때는 부분해를 구하는 과정이 최적해를 구하는 과정과 일치했고
현재 동전의 선택이 다른 과정에 영향을 주지 않았지만 배수가 아닐때는 그렇지 않았다.
따라서 어떤 문제에 그리디 알고리즘을 적용하고자 할 때는 두 가지 조건을 유의깊게 봐야한다.
배낭 문제(knapsak problem)
배낭 문제란, 배낭에 담을 수 있는 최대 무게가 존재하고, 무게와 가치가 다른 짐들이 있다고 할때, 배낭의 최대 무게를 초과하지 않으면서, 담은 가치를 최대로 하는 경우를 찾는 문제이다.
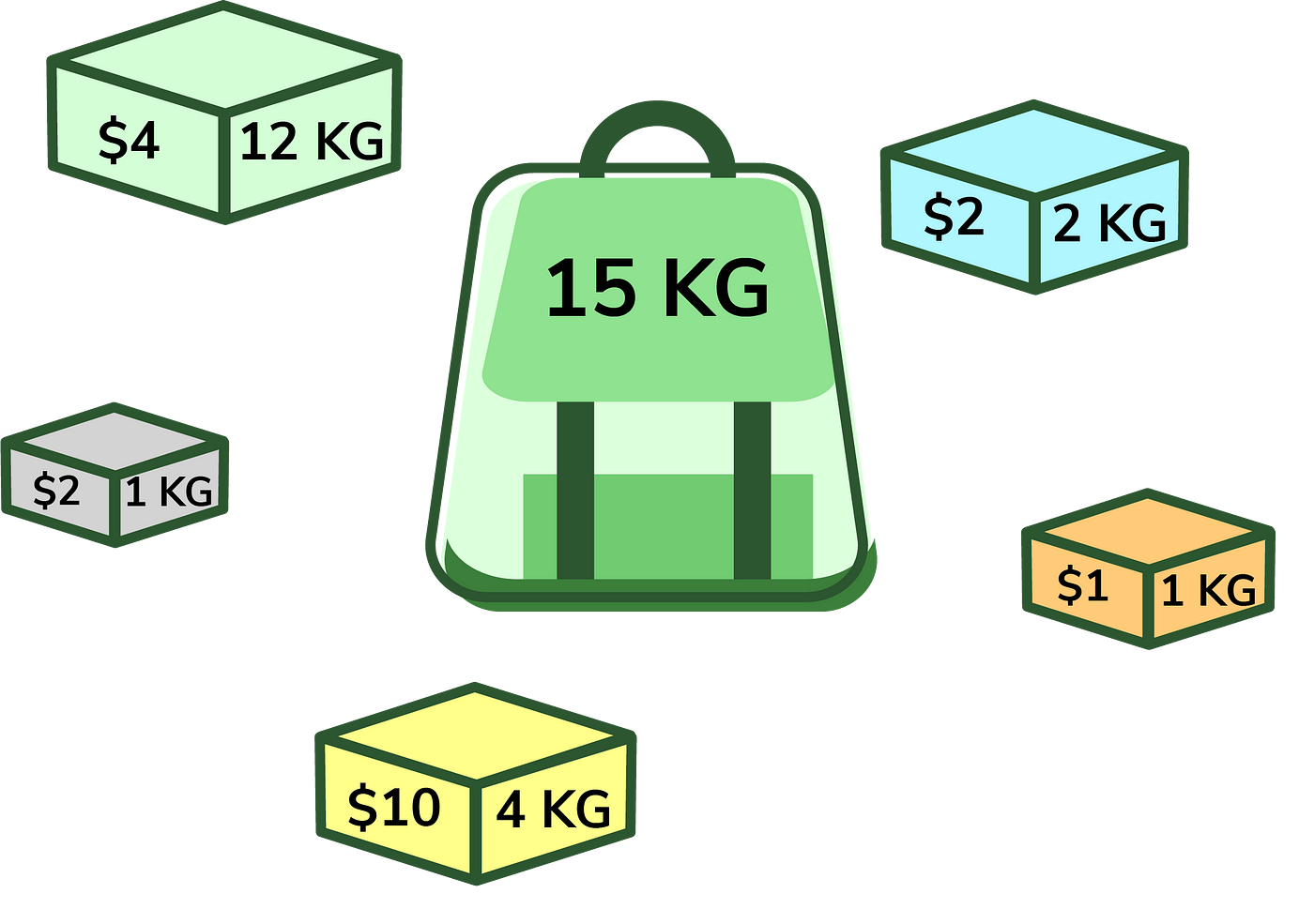
배낭 문제는 언뜻보면 동전문제와 비슷해보이지만 차이가 있다.
일단 배낭의 갯수가 1개이다.
또한 배낭의 무게 뿐아니라 가치가 있기 때문에 가치를 잘 따져가며 풀어야한다.
배낭 문제는 앞서 동전 문제와 마찬가지로 특정 상황에선 그리디로 풀 수 있고 특정 상황에선 풀 수 없다.
그게 어떤 상황인지 한번 보자.
그리디 알고리즘으로 풀 수 있는 경우
배낭 문제를 그리디 알고리즘으로 풀 수 있는 경우는 바로 배낭에서 부분적으로 짐을 꺼낼 수 있는 경우이다.

위와 같은 케이스를 그리디 알고리즘으로 접근해보자.
우선 배낭 문제의 최적의 해는 최고의 가치가 있는 배낭이기 때문에 각 배낭의 kg당 가치를 구해야 한다.
A. 1.9$/kg
B. 1.6..$/kg
C. 1.4..$/kg
구한 가치 순으로 배낭에 짐을 넣는다.
1) A(현재 배낭:15kg, 가치: $0)
현재 15kg가 남았기 때문에 10kg 배낭을 담을 수 있다.
배낭의 총 가치는 $19가 된다.
2) B(현재 배낭: 5kg, 가치: $19)
현재 5kg가 남았기 때문에 6kg 배낭을 담을 수 없다.
따라서 짐을 쪼개서 5kg만 넣어야 한다.
베낭의 총가치는 $27.33이 된다.
총가치: $27.33
이제 그리디 알고리즘으로 풀 수 없는 경우를 보자.
그리디 알고리즘으로 풀 수 없는 경우
베낭의 짐을 나누어서 넣을 수 없는 경우엔 그리디 알고리즘으로 풀 수 없다.

위와 똑같이 그리디로 풀어보자
1) A(현재 배낭:15kg, 가치: $0)
현재 15kg가 남았기 때문에 10kg 배낭을 담을 수 있다.
배낭의 총 가치는 $19가 된다.
2) B(현재 배낭: 5kg, 가치: $19)
현재 5kg가 남았기 때문에 6kg 배낭을 담을 수 없다.
짐을 쪼개서 넣을 수가 없기 때문에 넘어간다.
3) C(현재 배낭: 5kg, 가치: $19)
현재 5kg가 남았기 때문에 7kg 베낭을 담을 수 없다.
짐을 쪼개서 넣을 수가 없기 때문에 넘어간다.
그리디 답: $19
하지만 진짜 답은 B, C를 넣은 $20이다.
베낭문제 그리디 해결 조건
베낭 문제를 그리디로 해결하려면 앞서 말했듯, 베낭을 쪼갤 수 있어야한다.
쪼갤 수 없다면, 현재의 선택이 다른 선택에 영향을 미치게 되기 때문이다.
'코딩 테스트 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 동적 계획법(Dynamic Programming) (0) | 2024.06.24 |
|---|---|
| 행렬의 연산 (0) | 2024.06.22 |
| 정렬(Sort) (0) | 2024.06.19 |
| 백트래킹(BackTracking) 알고리즘 (0) | 2024.06.13 |
| 그래프 최단 경로 알고리즘 - 벨만 포드(Bellman-Ford) 알고리즘 (2) | 2024.05.31 |
