1. 행렬의 덧셈과 뺄셈
각 행렬에서 같은 위치에 있는 값끼리 더하거나 빼는 연산이다.
이때 두 행렬의 크기는 같아야 한다.
행렬의 덧셈과 뺄셈을 자바로 구현하면 다음과 같다.
// 행렬의 덧셈
public static void matrixSum(int[][] arr1, int[][] arr2) {
if(arr1.length != arr2.length || arr1[0].length != arr2[0].length){
System.out.println("두 행렬의 크기가 같지 않습니다.");
return;
}
int[][] result = new int[arr1.length][arr1[0].length];
for(int i = 0; i < arr1.length; i++) {
for(int j = 0; j < arr1[0].length; j++) {
result[i][j] = arr1[i][j] + arr2[i][j];
}
}
System.out.println("행렬의 덧셈 결과: ");
System.out.println(Arrays.deepToString(result));
}
// 행렬의 뺄셈
public static void matrixSub(int[][] arr1, int[][] arr2) {
if(arr1.length != arr2.length || arr1[0].length != arr2[0].length){
System.out.println("두 행렬의 크기가 같지 않습니다.");
return;
}
int[][] result = new int[arr1.length][arr1[0].length];
for(int i = 0; i < arr1.length; i++) {
for(int j = 0; j < arr1[0].length; j++) {
result[i][j] = arr1[i][j] - arr2[i][j];
}
}
System.out.println("행렬의 뺄셈 결과: ");
System.out.println(Arrays.deepToString(result));
}시간복잡도
- O(N^2)
2. 행렬의 곱셈
행렬의 곱셈에선 순서가 중요하다.

A->B 순서로 곱셈을 한다고 했을 때 A행렬의 열의 수가 B행렬의 행의 수가 같아야 성립한다.
이때 결과행렬의 행의 수는 A행렬의 행 수, 열의 수는 B행렬의 열 수가 된다.
또한 결과행렬의 (i,j)의 성분은 A행렬의 i번째 행과 B행렬의 j번째 열의 요소들을 각각 곱한뒤 더한 결과가 된다.
행렬의 곱셈을 자바로 구현하면 다음과 같다.
// 행렬의 곱셈
public static void matrixMult(int[][] arr1, int[][] arr2) {
if(arr1[0].length != arr2.length){
System.out.println("첫번째 배열의 열과 두번째 배열의 행의 수가 같아야 합니다.");
return;
}
int[][] result = new int[arr1.length][arr2[0].length];
for(int i = 0; i < arr1.length; i++) {
for(int j = 0; j < arr2[0].length; j++) {
for(int k = 0; k < arr1[0].length; k++) {
result += arr1[i][k] * arr2[k][j];
}
}
}
System.out.println("행렬의 곱셈 결과: ");
System.out.println(Arrays.deepToString(result));
}시간복잡도
- O(N^3)
3. 전치행렬
전치 행렬은 특정 행렬의 행과 열의 위치를 바꾼 행렬이다.
예를 들어 다음과 같은 행렬이 있다고 했을 때,

이 행렬의 전치 행렬은 다음과 같다.

전치행렬을 자바로 구현하면 다음과 같다.
public static void transposeMatrix(int[][] arr) {
int[][] result = new int[arr.length][arr[0].length];
for(int i = 0; i < arr.length; i++) {
for(int j = 0; j < arr[0].length; j++) {
result[i][j] = arr[j][i];
}
}
System.out.println("전치 행렬 결과: ");
System.out.println(Arrays.deepToString(result));
}시간복잡도
- O(N^2)
4. 행렬의 대칭
좌우 대칭

행이 N개 열이 M개 행렬에서 좌우 대칭을 일반화한다면 다음과 같다.
R[i, j] = A[i, M - j]
다만 구현시 인덱스가 0부터 시작하는걸 감안하면 다음과 같이 표현할 수 있다.
R[i, j] = A[i, M - 1 - j]
좌우 대칭을 자바로 구현하면 다음과 같다.
// 좌우 대칭
public static void symmetry(int[][] arr) {
int [][] result = new int[arr.length][arr[0].length];
int row = arr.length;
int col = arr[0].length;
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
result[i][j] = arr[i][col - 1 - j];
}
}
System.out.println("좌우 대칭 결과: ");
System.out.println(Arrays.deepToString(result));
}시간복잡도
- O(N^2)
상하 대칭
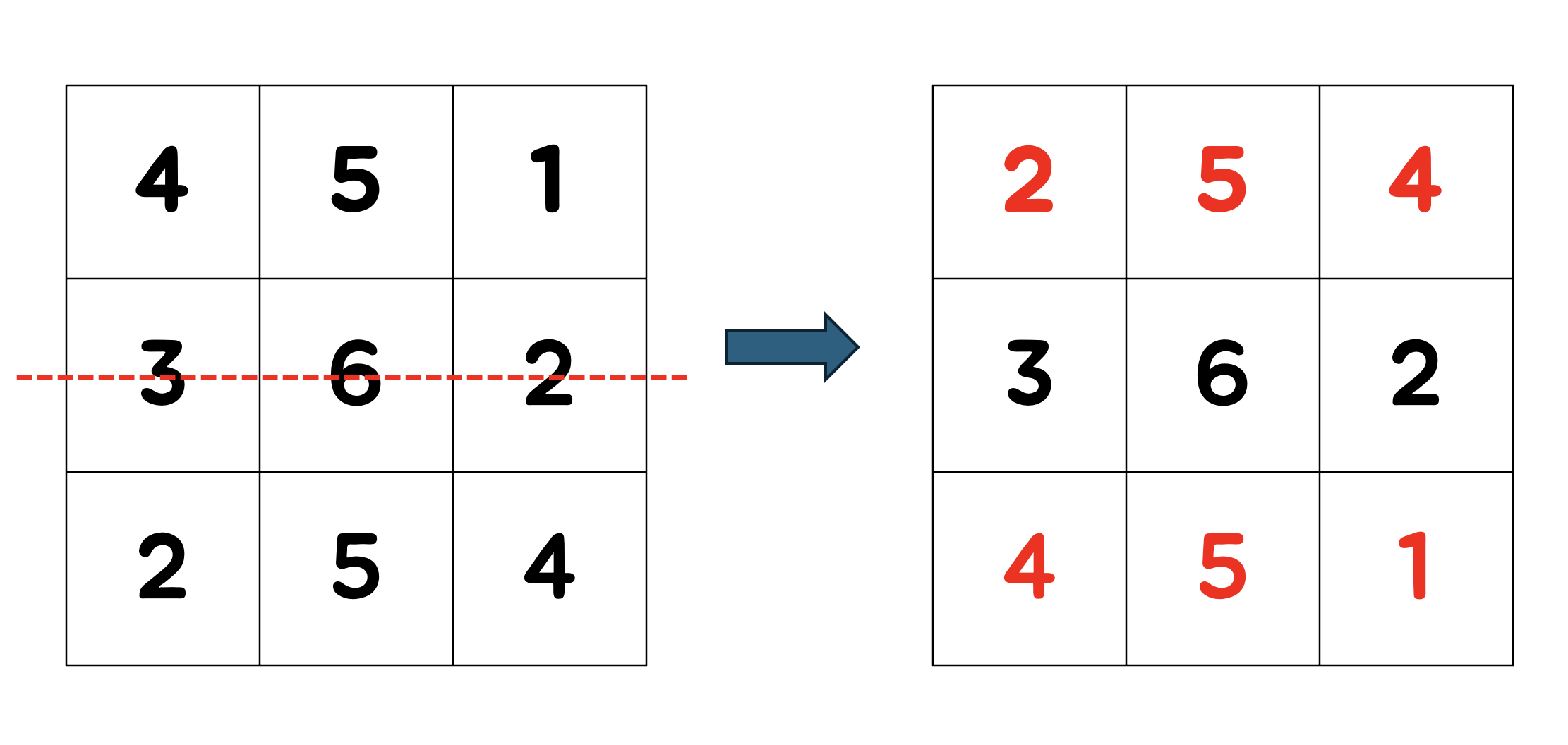
상하 대칭은 좌우 대칭의 반대라고 생각하면 된다.
행이 N개 열이 M개 행렬에서 좌우 대칭을 일반화한다면 다음과 같다.
R[i, j] = A[N - i, j]
다만 구현시 인덱스가 0부터 시작하는걸 감안하면 다음과 같이 표현할 수 있다.
R[i, j] = A[N - 1 - i , j]
상하 대칭을 자바로 구현하면 다음과 같다.
// 상하 대칭
public static void vertica_symmetry(int[][] arr) {
int [][] result = new int[arr.length][arr[0].length];
int row = arr.length;
int col = arr[0].length;
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
result[i][j] = arr[row - 1 - i][j];
}
}
System.out.println("상하 대칭 결과: ");
System.out.println(Arrays.deepToString(result));
}시간복잡도
- O(N^2)
5. 행렬 회전

행의 크기가 M이고 열의 크기가 N인 행렬에서 회전을 일반화하면 다음과 같다.
여기서 회전은 시계방향으로 90도 회전이다.
A[i, j] --> R[j, M - i]
구현시 인덱스가 0부터 시작하는 것을 감안하면
A[i, j] --> R[j, M - 1 - i]
반시계 방향 90도 회전의경우엔
A[i, j] --> R[N - j, i]
구현시 인덱스가 0부터 시작하는 것을 감안하면
A[i, j] --> R[N - 1 - j, i]
회전을 자바로 구현하면 다음과 같다.
// 시계방향 90도 회전
public static void rotate_clockwise(int[][] arr) {
int row = arr.length;
int col = arr[0].length;
int[][] result = new int[col][row];
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
result[j][row - 1 - i] = arr[i][j];
}
}
System.out.println("시계방향 90도 회전 결과: ");
System.out.println(Arrays.deepToString(result));
}
// 시계반대방향 90도 회전
public static void rotate_counterclockwise(int[][] arr) {
int row = arr.length;
int col = arr[0].length;
int[][] result = new int[col][row];
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
result[col - 1 - j][i] = arr[i][j];
}
}
System.out.println("시계반대방향 90도 회전 결과: ");
System.out.println(Arrays.deepToString(result));
}시간복잡도
- O(N^2)
6. 좌표 연산
2차원 좌표를 2차원 배열로 표현하기
2차원 좌표는 2차원 배열로 표현할 수 있다.
예를 들어 (3, 4)를 배열로 표현한다면 arr[4][3] = 1로 표현할 수 있다.
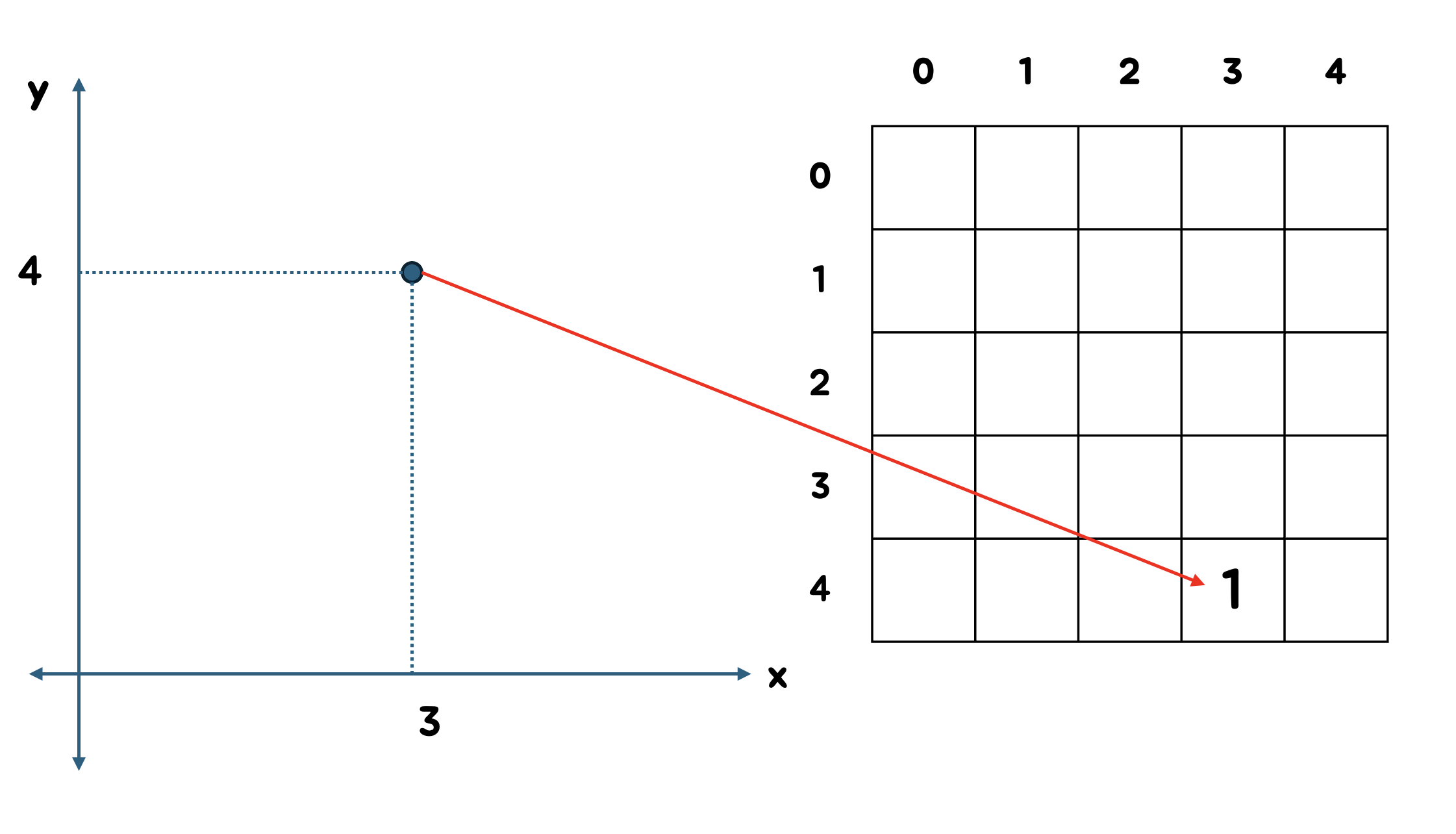
이를 일반화하면 좌표평면 (x, y)는 arr[y][x]로 표현할 수 있다.
하지만 좌표중 음수값을 가지는 좌표가 오면 2차원 배열에서는 음수인 인덱스가 없기 때문에 표현하기 힘들다.
이 경우, 좌표 값을 양수로 바꿔줘야 한다.
그 방법은 다음과 같다.
1. 주어진 좌표평면들에 대해서 x좌표의 최댓값, 최솟값, y좌표의 최댓값, 최솟값을 구한다.
2. 배열을 arr[y좌표의 최댓값 - 최솟값 + 1][x좌표의 최댓값 - 최솟값 +1]로 선언한다.
3. 좌표(x, y)를 arr[(x - x좌표의 최솟값), (y - y좌표의 최솟값)]에 저장한다.
좌표 이동을 오프셋값으로 표현하기
좌표를 활용하는 문제에서는 현재 위치를 이동하는 문제가 많은데 이때 오프셋값으로 표현해 사용하면 깔끔하게 코드를 짤 수 있다.
다음과 같이 현재 위치 0에서 1~8로 이동하는 상황을 구현해야 한다면

이때, 현재 위치가 arr[cur_y][cur_x]라면 각 위치는 다음과 같다.
- 1위치: arr[cur_y - 1][cur_x - 1]
- 2위치: arr[cur_y - 1][cur_x]
- 3위치: arr[cur_y - 1][cur_x + 1]
- 4위치: arr[cur_y][cur_x - 1]
- 5위치: arr[cur_y][cur_x + 1]
- 6위치: arr[cur_y + 1][cur_x - 1]
- 7위치: arr[cur_y + 1][cur_x]
- 8위치: arr[cur_y + 1][cur_x + 1]
이러한 변화를 별도의 오프셋 배열로 선언한다면 다음과 같다.
int[] dy = {-1, -1, -1, 0, 0, 1, 1, 1};
int[] dx = {-1, 0, 1, -1, 1, -1, 0, 1};
이제 반복문을 사용하면 효율적으로 1~8방향으로 이동할 수 있다.
int[] dy = {-1, -1, -1, 0, 0, 1, 1, 1};
int[] dx = {-1, 0, 1, -1, 1, -1, 0, 1};
for(int i = 0; i < 8; i++){
arr[cur_y + dy[i]][cur_x + dx[i]];
}
'코딩 테스트 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 그리디(Greedy) 알고리즘 (0) | 2024.06.25 |
|---|---|
| 동적 계획법(Dynamic Programming) (0) | 2024.06.24 |
| 정렬(Sort) (0) | 2024.06.19 |
| 백트래킹(BackTracking) 알고리즘 (0) | 2024.06.13 |
| 그래프 최단 경로 알고리즘 - 벨만 포드(Bellman-Ford) 알고리즘 (2) | 2024.05.31 |
