해시(Hash)란?
해시(Hash)란 특정 key를 인덱스로 삼아 value 값을 저장하는 자료구조이다.
이 key 값은 해시함수를 통해 해시값으로 변환되어 value값의 인덱스가 된다.
리스트와 같은 자료구조에선 단순히 숫자가 value의 인덱스가 되겠지만 해시에는 숫자 뿐만 아니라 모든 객체를 인덱스처럼 사용할 수 있다.
이러한 자료구조는 실생활에서도 쉽게 볼 수 있는데 대표적인 예가 전화번호부이다.

- key가 이름이고 value가 전화번호이다.
- 이름을 해시함수에 넣어서 이를 통해 해시 값을 반환해 전화번호에 매핑한다.
해시를 통해 빠르게 특정 데이터를 빠르게 접근할 수 있다.
key값만 있으면 value값을 바로 찾아낼 수 있으므로 시간 복잡도가 O(1)이 된다.
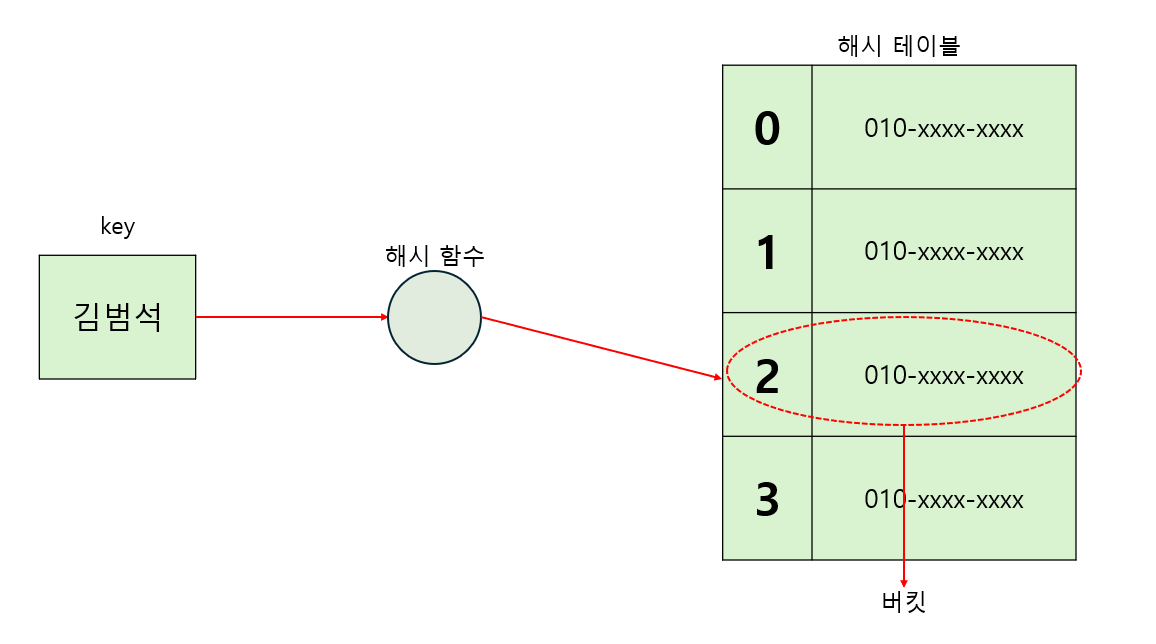
- 해시 값과 value를 매칭시켜놓은 공간을 해시테이블이라고 한다.
- 해시 테이블의 각각의 데이터를 버킷이라고 한다.
해시 함수
해시에서는 해시함수를 통해 key값을 해시값으로 변환한다.
좋은 해시함수가 되기 위해선 다음의 특징을 만족해야 한다.
- 해시함수의 반환 값은 0부터 해시 테이블의 크기-1 사이여야 한다.
- 해시 충돌이 적게 일어나야 한다.
1번을 만족하지 않게 되면 key에 대한 정확한 value값을 찾을 수 없고 해시 테이블에서 벗어나는 해시 값을 반환할 수 있다.
2번의 해시 충돌이란 서로 다른 key 값에 대해 같은 해시값을 반환하는 경우를 말하는데 이 해시 충돌이 적게 일어나야 한다. 여기서 적게라는 말을 쓴 것은 아예 해시 충돌이 일어나지 않는 해시함수는 없다는 뜻이다.
이제부터 해시함수의 종류에 대해 알아보자
1. key가 숫자인 경우
1. 나눗셈법
나눗셈법은 가장 기본적인 해시 함수이다.

- x: key
- k: 소수(해시 테이블의 크기)
나눗셈법의 핵심은 k가 소수여야 한다는 점이다.
예를 들어 k가 합성수인 15이고 x가 15의 약수 중 하나인 3의 배수인 경우 해시값 3, 6, 9, 12, 0이 무한 반복된다.
또 x가 15의 또 다른 약수인 5의 배수인 경우 해시값 5, 10, 0이 무한 반복된다.
이렇게 되면 해시 충돌이 일어날 확률이 올라간다.
따라서 k는 반드시 소수여야 한다.
이때 k는 해시 테이블의 크기이다.
해시 테이블의 크기는 버킷의 개수가 근사한 소수값으로 결정되게 되는데 데이터 갯수가 많아지면 큰 소수를 계산해야 한다. 이 큰 소수를 찾아내는 연산은 매우 오래걸리는 작업이기 때문에 데이터 갯수가 많아지면 효율성이 떨어진다.
이 부분이 바로 나눗셈법의 단점이다.
2. 곱셈법
곱셈법은 나눗셈법의 단점을 보완한 해시 함수이다.
곱셈법은 나눗셈법 단점의 원인이었던 소수를 사용하지 않는다.
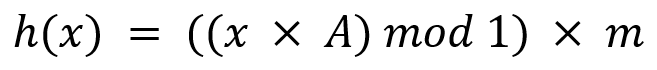
- x: key
- A: 황금비의 소수 부분(황금비: 1.618033. 연산시엔 0.6183만 사용)
- m: 해시 테이블의 크기
1. key값인 x에 황금비의 소수부분인 0.6183을 곱한다.
2. 1의 결과에 mod 1을 한다.
참고로 mod 1은 정수부분을 제거하고 소수부분만 취하는 연산이다.
3. 2의 결과에 해시 테이블의 크기인 m을 곱한 뒤 정수부분을 취한다.
결과는 0 ~ m - 1사이로 나오게 된다.
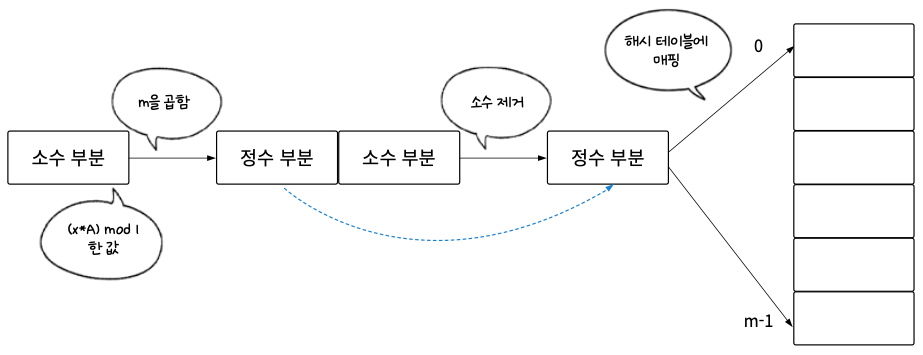
이렇게 곱셈법을 사용하면 소수를 사용하지 않기 때문에 해시 테이블의 크기가 커져도 부담이 줄어든다.
2. key가 문자열인 경우
문자열 해싱
문자열을 key값으로 사용하는 경우 문자열의 각 문자를 숫자로 바꿔야 한다.
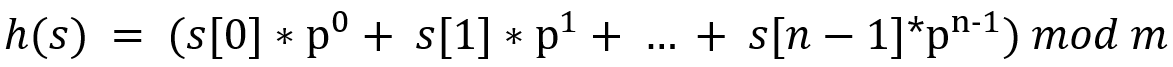
- s: key
- s[i]: 문자열 s의 i번째 문자를 숫자로 변환한 값
- p: 31(메르센 소수)
- 메르센 소수는 2^n -1 형식으로 표시할 수 있는 숫자 중 소수인 수를 말함
- 메르센 소수는 해시에서 충돌을 줄이는데 효과적이라는 연구 결과가 있음
- m: 해시 테이블의 크기
1. 문자열의 각 문자를 숫자로 변환한다.
알파벳의 경우 일반적으로 a~z까지를 1~26으로 매치한다.
2. 문자열의 각 문자에 대한 적절한 메르센 소수의 제곱수를 곱한다.
i번째 문자인 경우 p^i를 곱한다.
3. 이렇게 곱한 수를 다 더한 뒤 m으로 모듈러 연산을 한다.
만약 키가 twins고 m이 10이라면

하지만 이렇게하면 문제점이 하나 발생한다.
위의 Twins같은 간단한 단어 하나에도 더했더니 17,973,355가 나왔다. 문자열이 조금 더 길어지면 오버플로우가 일어날 것이다.
따라서 위의 공식을 다음과 같이 수정해야 한다.

위의 공식은 다음 공식이 성립함에 의거하여 수정된 것이다.
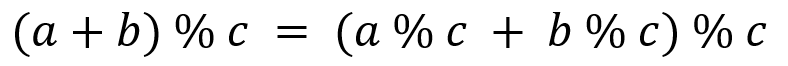
해시 충돌 처리
해시 충돌이란 해시 충돌이란 서로 다른 key 값에 대해 같은 해시값을 반환하는 경우를 말한다.
아무리 좋은 해시함수를 사용해서 해시 충돌은 발생하기 마련이다.
지금부터 이러한 해시충돌을 해결하는 방법에 대해 알아보자
체이닝
체이닝은 해시 충돌을 해결하는 가장 기본적인 방법이다.
해시 충돌이 발생하면 해당 버킷에 링크드리스트로 데이터를 연결한다.
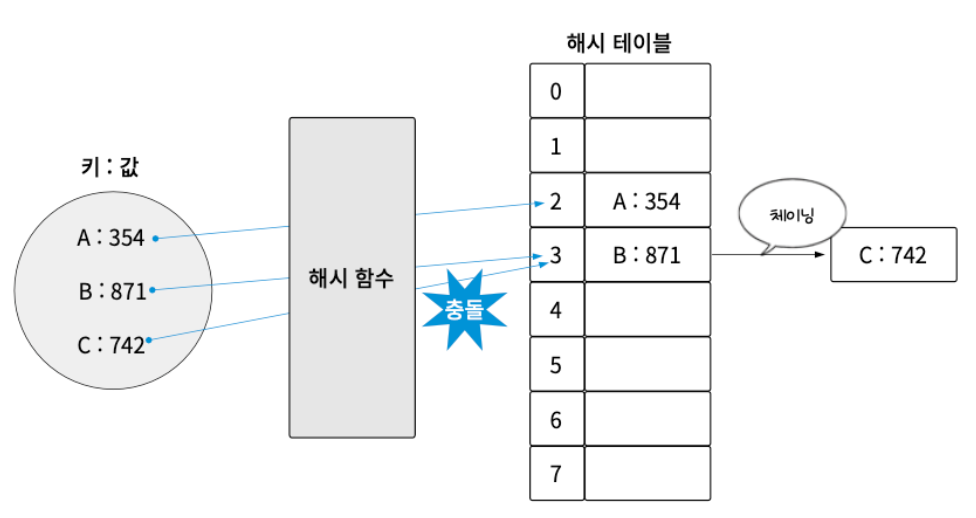
하지만 체이닝 방식은 두 가지 단점이 있다.
1. 해시 테이블 공간 활용성이 떨어진다.
해시 충돌이 많아지면 링크드 리스트의 길이가 길어지고 다른 해시테이블의 공간을 사용하지 않게 돼 공간활용성이 떨어지게 된다.
2. 검색 성능이 떨어진다.
링크드리스트에서 데이터를 검색하려면 순차적으로 접근해야 하기 때문에 O(N)의 시간복잡도가 발생한다.
이렇게 되면 해시를 쓰는 이유가 사라지는 것이다.
개방 주소법
개방 주소법은 해시 충돌 발생시 링크드 리스트를 통해 데이터를 저장하는 것이 아닌 해시 테이블의 빈 버킷을 찾아 저장한다.
1. 선형 탐사 방식
선형 탐사 방식이란 해시 충돌이 발생하면 발생한 곳으로부터 일정한 간격으로 빈 버킷을 찾을 때까지 움직이는 것을 말한다.
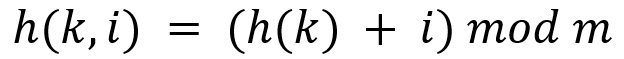
- h(k): 해시 함수
- k: key
- i: 빈 버킷을 찾기 위해 움직일 간격
- m: 해시 테이블의 크기
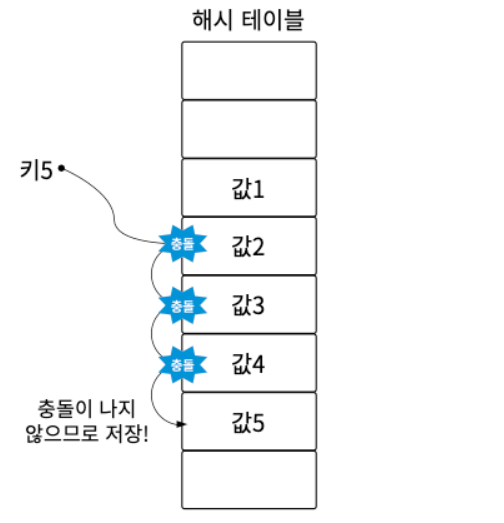
하지만 선형 탐사 방식의 경우 충돌이 발생할 때 마다 일정한 간격으로 빈 버킷을 찾아 데이터를 저장하게 되면 데이터가 특정 부분에 모이게 되는 현상이 발생한다. 이를 클러스터를 형성한다고 하는데 이 클러스터가 생기게 되면 해시 충돌이 발생할 확률이 올라가서 좋지 않다.
2. 이중 해시 방식
이중 해시 방식은 선형 해시 방식의 단점을 보완한 방식이다.
이중 해시 방식은 해시 충돌이 일어나면 별도의 해시 함수를 한번 더 적용해 간격을 산발적으로 발생시키는 방식이다.
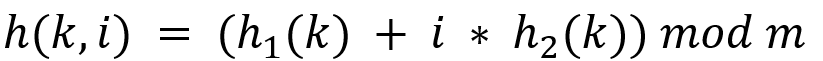
- k: key
- i: 2차 해시 함수를 적용한 횟수 (0, 1, ...)
- h(): 해시 함수
- m: 해시 테이블의 크기
1. 먼저 1차 해시함수를 통해 해시 값을 구한다.
1-1. 만약 해시 충돌이 일어나지 않는다면 해당 위치에 데이터를 저장한다.
1-2. 만약 해시 충돌이 일어나면 2차 해시 함수를 사용한다.
2. (1에서 해시 충돌이 일어난 경우) 2차 해시 함수를 통해 구한 값에 i를 곱한다.
이때 i는 2차 해시 함수를 실행시킨 횟수 이다.
해시 충돌이 일어날 때마다 i를 증가시킨다.
3. 추후에 해시 충돌이 일어날 때마다 i값을 증가 시켜 해시 값을 구한다.
일반적으로 사용하는 h1, h2 해시함수는 다음과 같다.
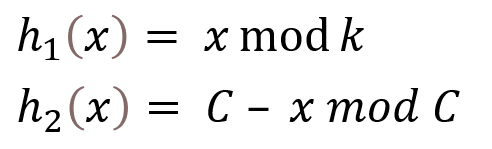
이때 k와 c는 서로소 관계여야한다.
자바의 해시맵(HashMap)
지금까지 전반적인 해시의 개념에 대해 알아봤다.
지금부터는 코딩 테스트에서 해시를 사용하는 방법에 대해 알아보자
자바에선 HashMap 클래스를 통해 해시를 사용할 수 있다.
HashMap<KeyType, ValueType> hashMap = new HashMap<>();
해시맵의 ADT
| 메서드 | 기능 |
| ValueType put(KeyType key, ValueType value) | key, value를 해시맵에 저장한다. 만약에 key가 이미 기존에 해시맵에 있다면 그 key와 value를 새로운 key, value로 대체하고 기존의 value를 반환한다. |
| ValueType get(KeyType key) | key에 해당하는 value를 반환한다. |
| ValueType remove(KeyType key) | key와 그 key에 해당하는 value를 지운뒤 value를 반환한다. |
| boolean containsKey(KeyType key) | key가 해시맵에 저장되어 있다면 true 없다면 false를 반환한다. |
| void clear() | 해시맵에 모든 데이터를 삭제한다. |
| boolean isEmpty() | 해시맵이 비어있다면 true 비어있지 않다면 false를 반환한다. |
| int size() | 해시맵의 데이터 갯수를 반환한다. |
연습문제
[프로그래머스] 두 개의 수로 특정값 만들기
1. 문제 2. 풀이 과정이 문제를 딱보자마자 들었던 생각은 이중 for문 이었다.이중 for문을 통해 두 개의 수를 뽑아서 합을 구한 다음, 그 합이 target과 일치하는지를 확인하면 된다.그렇게 되면
jaehee1007.tistory.com
해당 포스트는 『코딩 테스트 합격자 되기 - 자바편』을 참고하여 작성되었습니다.
'코딩 테스트 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 상호베타적(서로소) 집합과 유니온 파인드 알고리즘 (0) | 2024.05.24 |
|---|---|
| 이진 탐색 트리(Binary Search Tree) (0) | 2024.05.21 |
| 트리(Tree) (0) | 2024.05.21 |
| 큐(Queue) (0) | 2024.05.04 |
| 스택(Stack) (0) | 2024.04.28 |
