상호베타적(서로소) 집합이란?
상호베타적 집합(또는 서로소 집합: Disjoint Set)이란 교집합이 없는 집합관계를 의미한다.
상호베타적 집합은 다음과 같이 트리 형태로 표현한다.

집합 A와 B는 교집합이 존재하지 않으므로 상호베타적 집합이라고 할 수 있다.
상호베타적 집합 표현하기
상호베타적 집합은 위에서 봤듯 트리 구조로 표현할 수 있다.
이에 대해 더 자세히 알아보도록 하자.
대표원소
상호베타적 집합에서 각각의 집합에는 대표원소라는 것이 존재한다.
대표원소는 트리의 루트노드에 해당한다.

상호베타적 집합을 배열로 구현하기
트리구조로 표현한 상호베타적 집합은 배열로 구현할 수 있다.
방법은 간단하다.
배열에 자신의 부모 노드에 해당하는 원소값을 넣으면 된다.
루트노드일 경우에는 자신의 원소값을 넣는다.
그림으로 보도록하자.

- 교집합이 없기 때문에 두 집합을 하나의 배열로 표현할 수 있다.
- 배열의 크기는 원소의 최대 값보다 하나 더 크게 설정한다.(인덱스가 0부터 이므로)
- 0과 7의 경우엔 어느집합에도 존재하지 않으므로 -1로 설정했다.
- 1과 4는 루트노드 이므로 자신의 값을 할당한다.
- 2, 3은 부모노드가 1이므로 1을 할당한다.
- 5, 6은 부모노드가 4이므로 4를 할당한다.
- 8은 부모노드가 6이므로 6을 할당한다.
유니온 파인드(Union-Find) 알고리즘
위에서 상호베타적 집합을 트리로 표현하고 배열로 구현한 이유는 바로 이 유니온 파인드 알고리즘을 효율적으로 구현하기 위함이다.
유니온 파인드 알고리즘이란 상호베타적 집합을 활용하는 알고리즘이다.
이름에서도 알 수 있듯 유니온 파인드 알고리즘은 두 가지 알고리즘으로 이루어져 있다.
바로 유니온(Union) 알고리즘과 파인드(Find) 알고리즘이다.
이름 순서상 유니온(Union) 알고리즘이 먼저 나오지만 파인드(Find) 알고리즘을 먼저 설명해야 이해가 쉽기 때문에 파인드 알고리즘부터 설명하겠다.
파인드(Find) 알고리즘
Find 알고리즘은 특정 원소의 루트 원소를 찾는 알고리즘이다.
과정은 다음과 같다.
1. 현재 노드의 부모 노드를 찾는다.
2. 부모노드가 루트노드인지 확인한다.
3. 1,2의 과정을 루트노드가 나올 때까지 반복한다.
예를 들어 8에 대해 파인드(Find) 알고리즘을 수행한다면
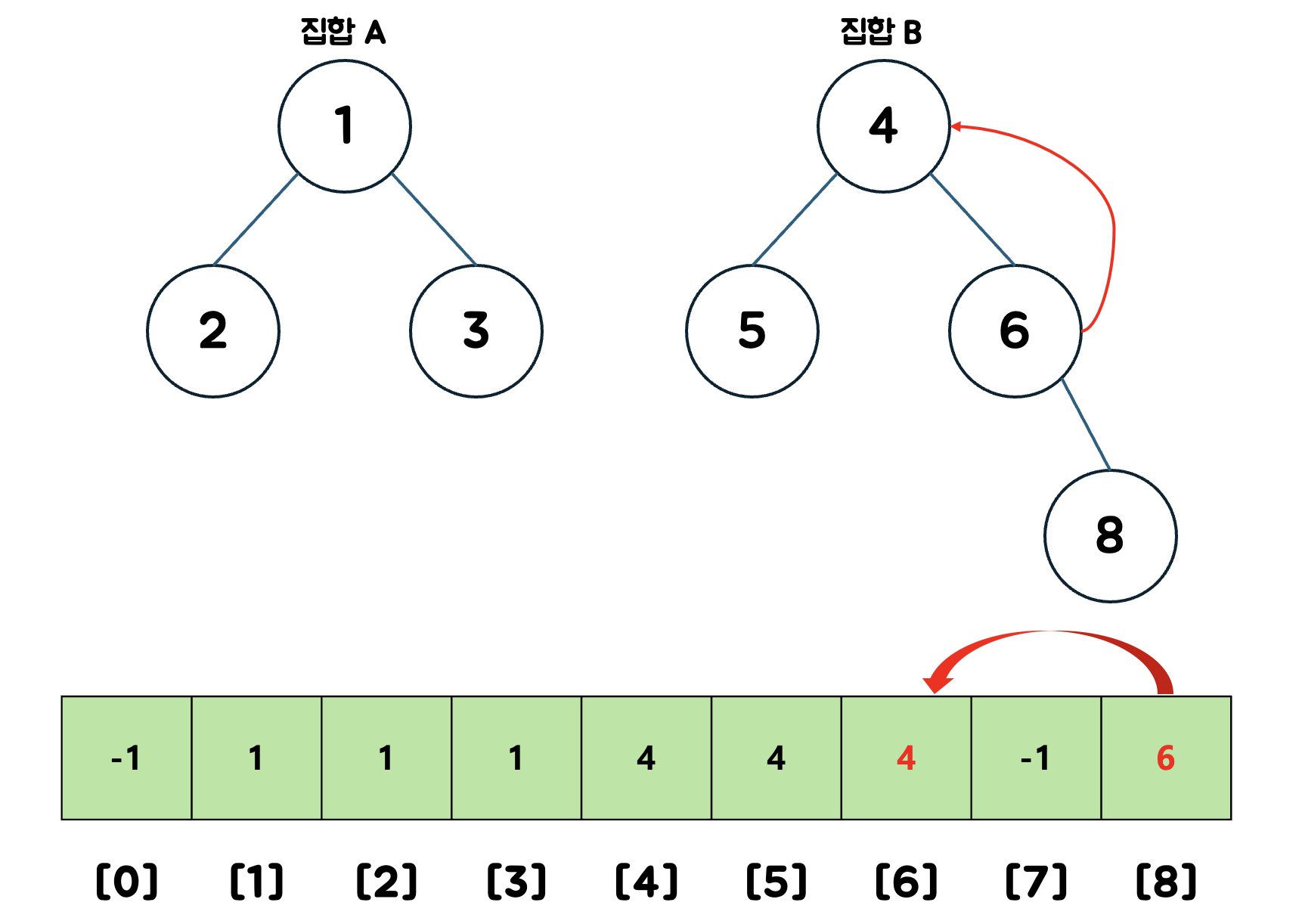
배열을 통해 8의 부모 노드를 확인한다.
6은 루트노드가 아니므로 6을 현재노드로 설정한다.
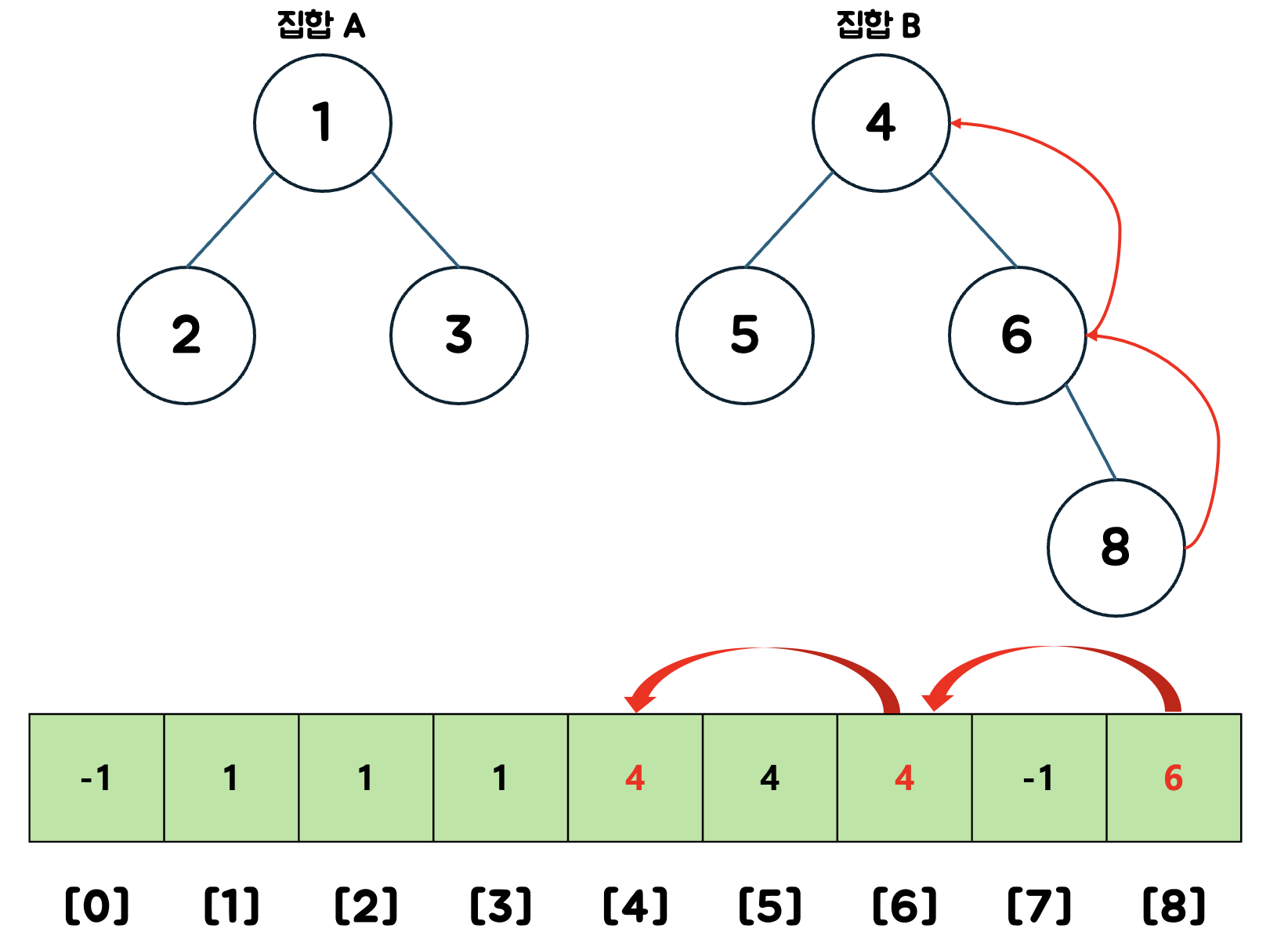
배열을 통해 6의 부모 노드를 확인한다.
4는 배열의 값과 인덱스 값이 같다. 즉, 루트노드라는 의미이다.
위에서 보았듯, 배열을 재귀적으로 순회하면 빠르게 루트노드를 찾을 수 있다.
유니온(Union) 알고리즘
유니온(Union) 알고리즘은 상호베타적 집합 관계에 있는 두 집합을 합치는 알고리즘이다.
두 집합을 합친다는 것은 루트노드를 같게 한다는 것이다.
이 말을 달리 말하면 한 집합을 다른 집합 아래에 갖다 붙이기만 하면 된다는 의미이다.
세부적인 과정은 다음과 같다.
1. 각 집합의 루트 노드를 찾는다.
(이 과정은 파인드(find) 알고리즘을 이용하면 된다.)
2. 두 집합을 합친다.
(두 집합의 루트노드를 같게한다. 이때, 루트노드는 두 집합 중 어떤 루트 노드로 해도 상관 없다.)
그림으로 보도록하자
1. 각 집합의 루트 노드를 찾는다.

집합 A는 1이고 집합 B는 4이다.
이 과정은 파인드(find)알고리즘을 사용하면 된다.
2. 두 집합을 합친다.
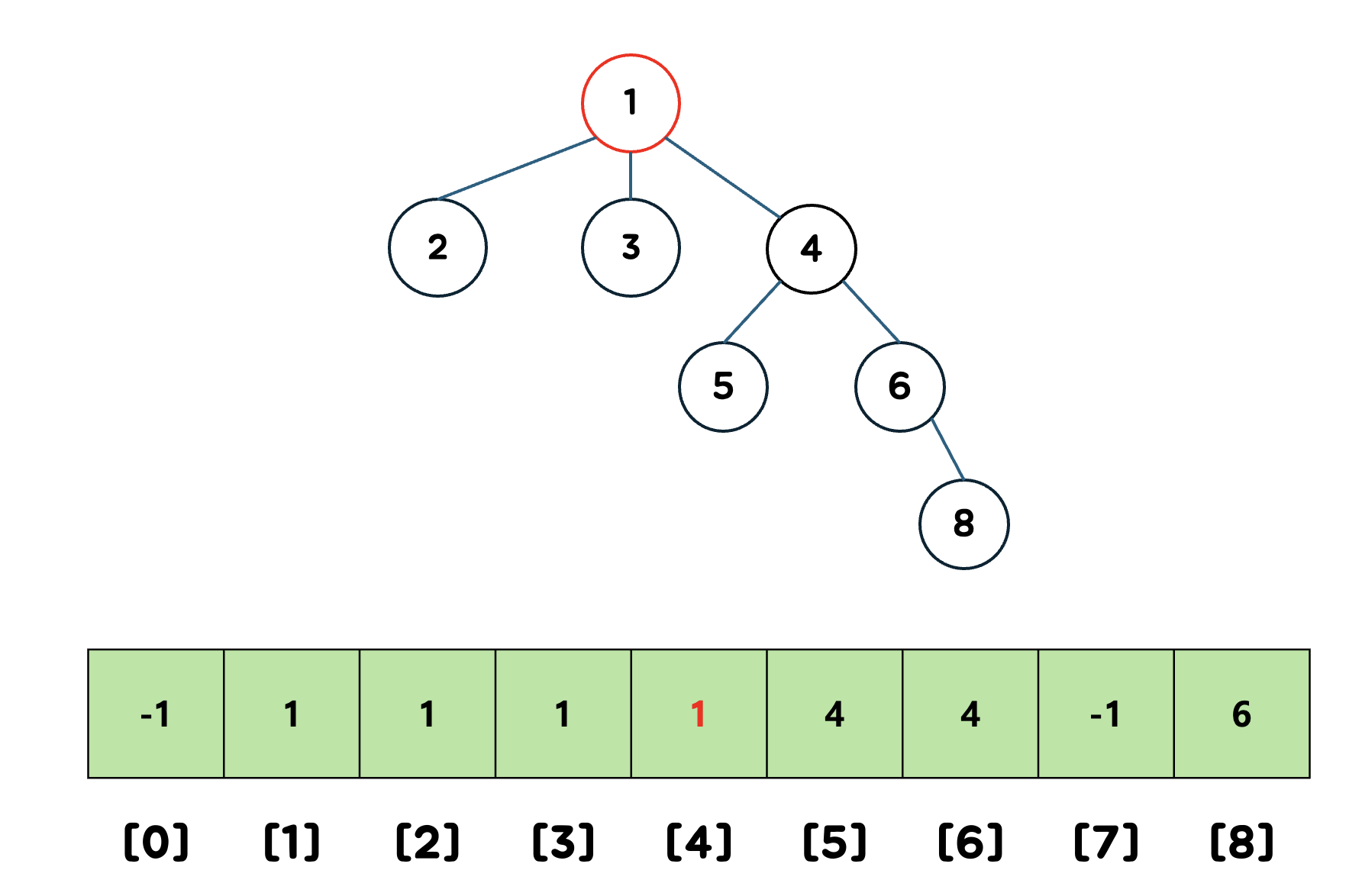
여기선 집합 A의 루트노드로 통일했다.
집합 B의 루트 노드였던 4의 값을 1로 바꿔주면 끝난다.
랭크를 통한 유니온(Union) 알고리즘 성능 향상 시키기
위에서 설명한 유니온 알고리즘은 트리의 깊이가 깊어질수록 연산비용이 커진다는 단점이 있다.
이를 개선하기 위해서 랭크라는 개념을 사용한다.
랭크란?
랭크란 현재 노드에서 가장 깊은 노드까지의 경로길이를 의미한다.
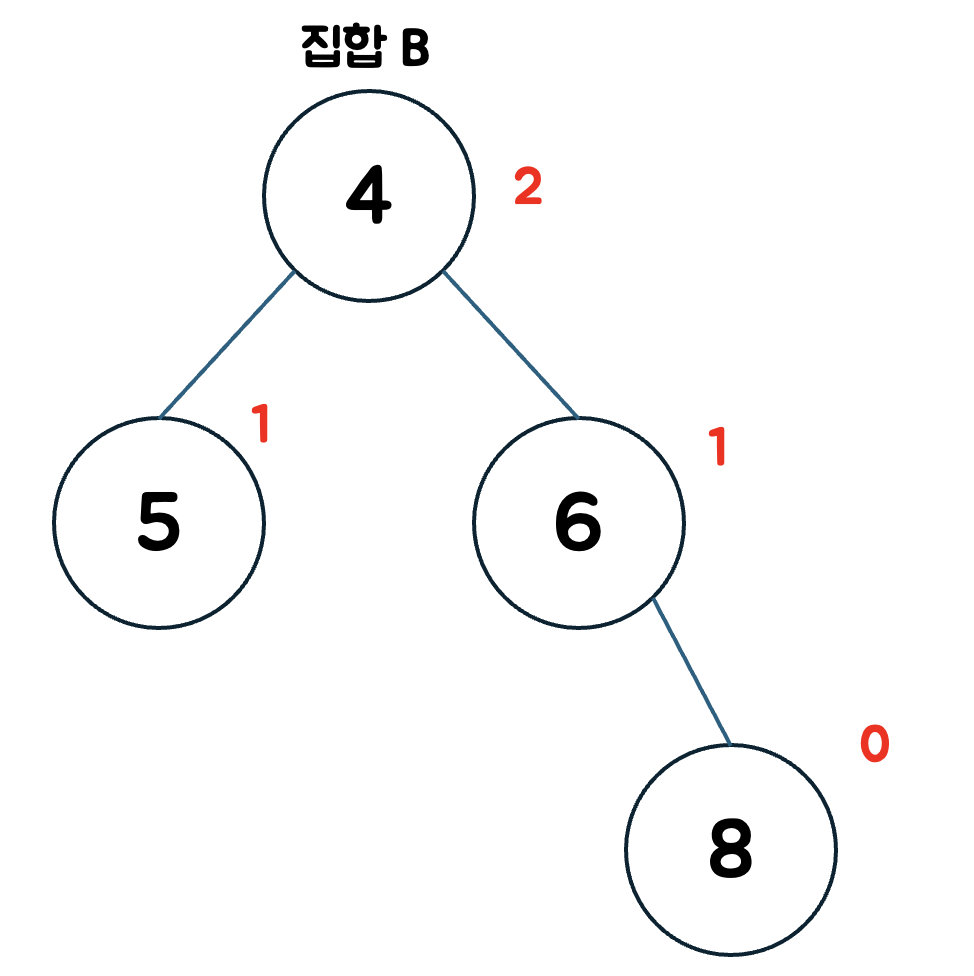
해당 집합에서 루트노드 4의 랭크는 2이다.
루트노드의 랭크가 커질수록 유니온(Union) 알고리즘의 효율은 떨어진다.
그렇기 때문에 루트노드를 통일시킬 때 아무 집합의 루트노드로 통일시키는 것이 아닌
루트노드의 랭크를 비교하여 랭크가 더 작은 집합의 루트노드로 통일시켜야 한다.
랭크를 도입한 유니온 알고리즘(Union)의 과정을 보자.
1. 각 집합의 루트 노드를 찾는다. (이 과정은 파인드(find) 알고리즘을 이용하면 된다.)
2. 두 루트노드의 랭크를 비교한다
2-1. 랭크 값이 다르면 더 큰 루트 노드를 루트노드로 한다.
2-2. 랭크 값이 같으면 두 루트 노드 중 아무 루트노드를 루트노드로 한다.
위의 예시를 다시보면
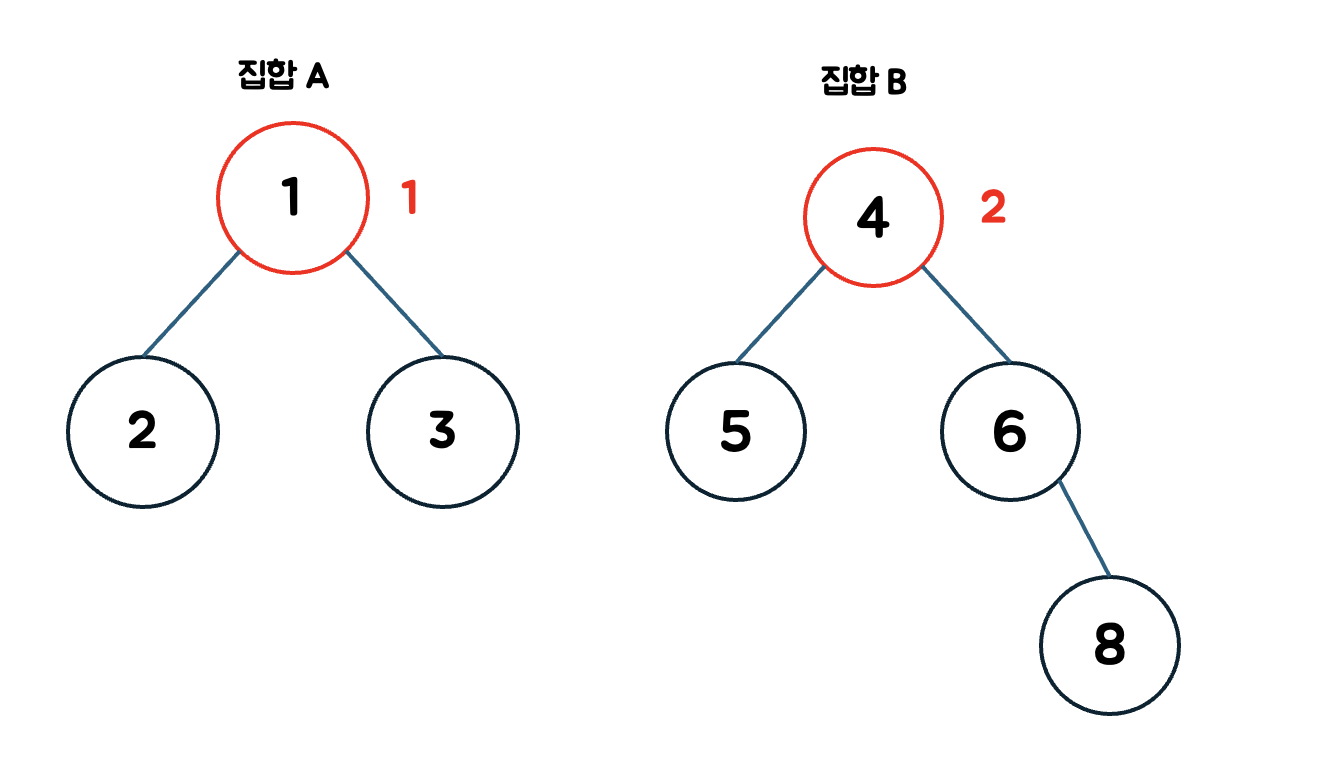
집합 A 루트노드의 랭크는 1이고 집합 B 루트노드의 랭크는 2이다.
그러므로 더 큰 B의 루트노드를 루트노드로한다.
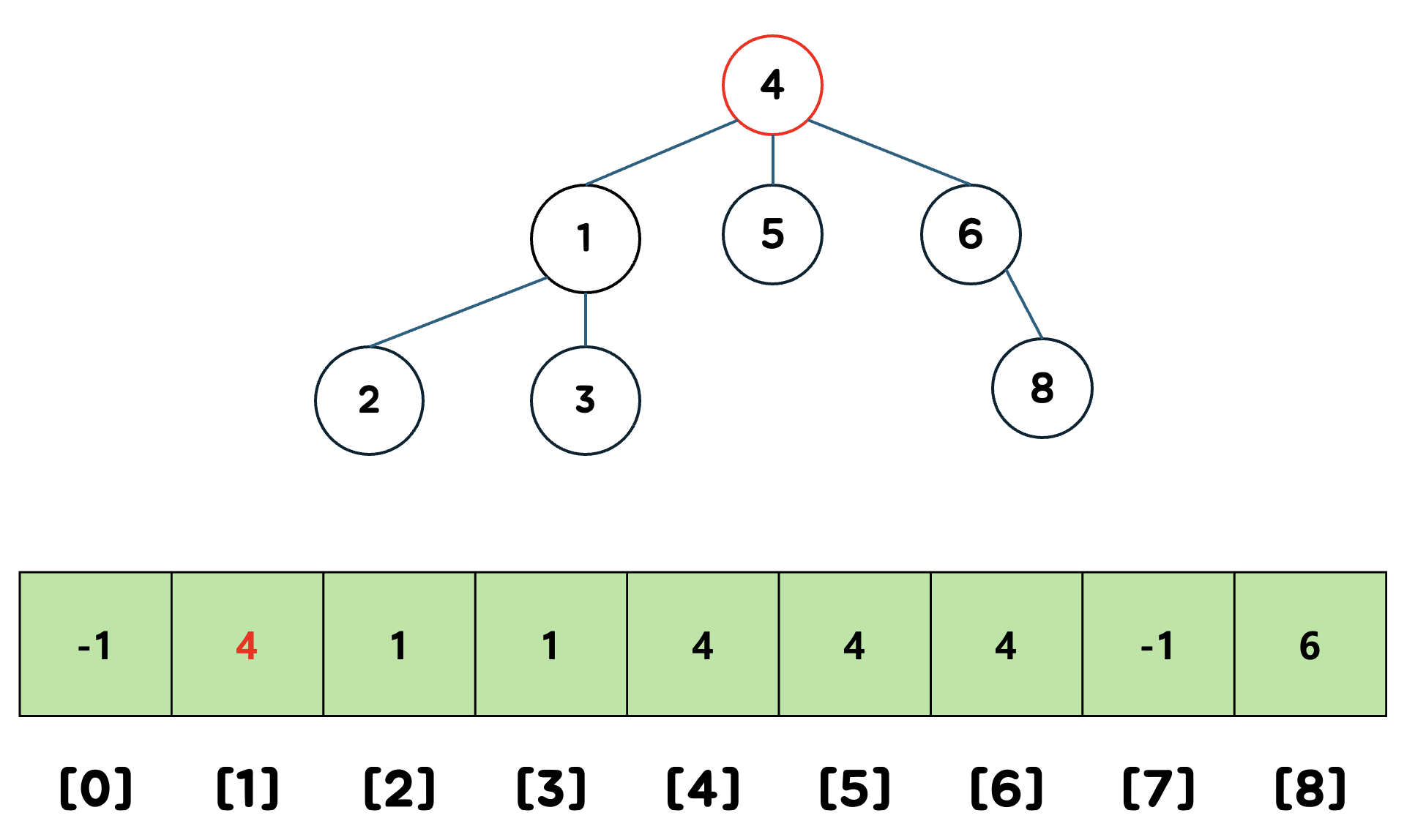
1의 배열 값을 4로 업데이트 한다.
유니온 파인드 알고리즘 구현하기(자바)
자료구조
int[] parent;
int[] rank;- parent[]: 각 원소의 부모 원소
- rank[]: 각 원소의 랭크
파인드(Find) 알고리즘
int find(int val) {
if (parent[val] == val) {
return val;
}
return find(parent[val]);
}- 해당 원소의 부모 원소를 찾고 그 원소가 루트 노드인지를 재귀적으로 확인한다.
유니온(Union) 알고리즘
void union(int x, int y) {
int root_x = find(x);
int root_y = find(y);
if(root_x != root_y) {
if(rank[root_x] > rank[root_y]) {
parent[root_y] = root_x;
} else if(rank[root_x] < rank[root_y]) {
parent[root_x] = root_y;
} else {
parent[root_y] = root_x;
rank[root_x]++;
}
}
}- 먼저 두 집합의 루트 노드를 찾는다.
- 이후 두 루트노드의 랭크를 비교해서 랭크가 큰 루트노드를 루트노드로 한 뒤 합친다.
- 랭크가 같으면 임의의 루트노드를 루트노드로 한다.
활용사례
유니온 파인드 알고리즘은 다양한 사례에서 활용되고 있다.
대표적으로 최소신장트리를 구할 때 그래프의 사이클 여부를 검토할 때 활용된다.
해당 포스트는 『코딩 테스트 합격자 되기 - 자바편』을 참고하여 작성되었습니다.
'코딩 테스트 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 그래프의 탐색(깊이 우선 탐색과 너비 우선탐색) (0) | 2024.05.29 |
|---|---|
| 그래프 (Graph) (0) | 2024.05.29 |
| 이진 탐색 트리(Binary Search Tree) (0) | 2024.05.21 |
| 트리(Tree) (0) | 2024.05.21 |
| 해시 (Hash) (0) | 2024.05.06 |
