이진 탐색 트리(Binary Search Tree)
이진 탐색 트리란?
이진 탐색 트리는 다음의 두 가지 조건을 만족하는 이진 트리이다.
1. 왼쪽 자식노드들은 자신의 부모 노드보다 작다.
2. 오른쪽 자식노드들은 자신의 부모 노드보다 크다(같을 때도 오른쪽).

이러한 배치는 트리에서 특정 데이터를 찾거나 삭제할 때 매우 유용하다.
탐색
예를 들어 4라는 값을 찾는다고 가정해보자
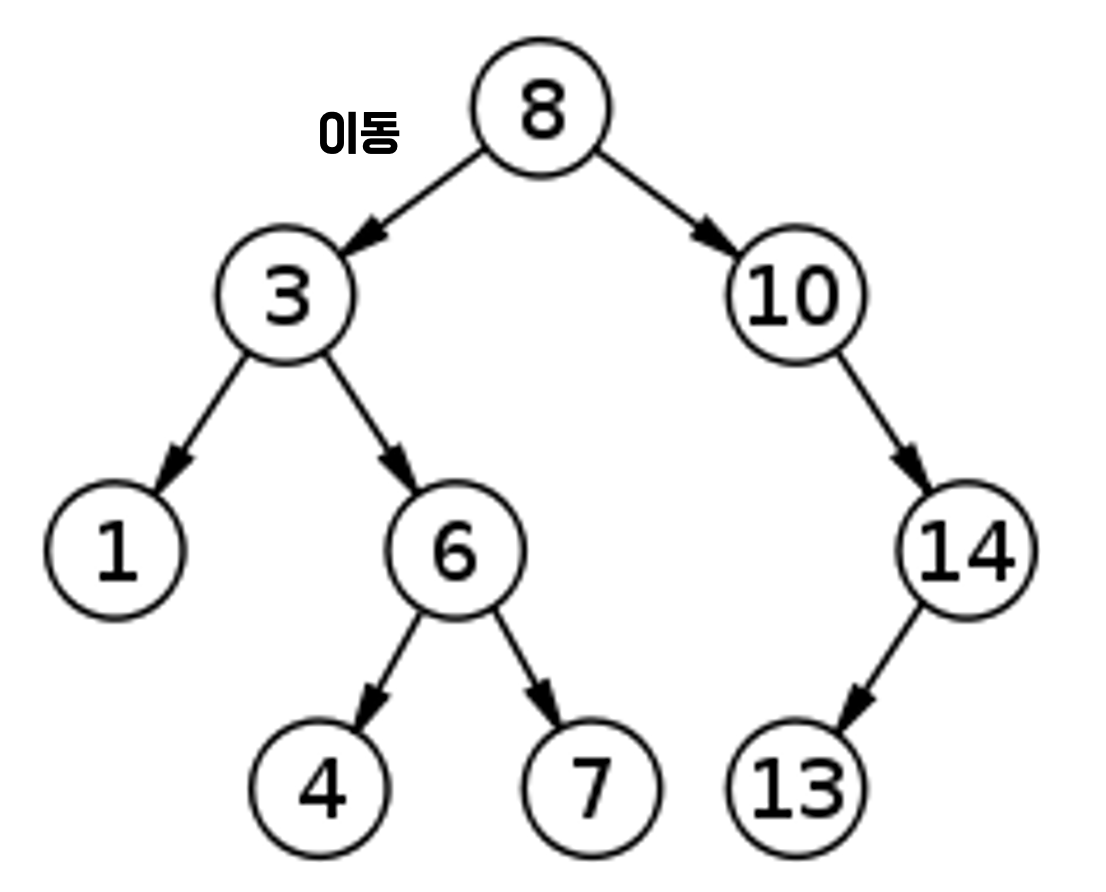
- 4는 8보다 작으므로 왼쪽으로 이동한다.
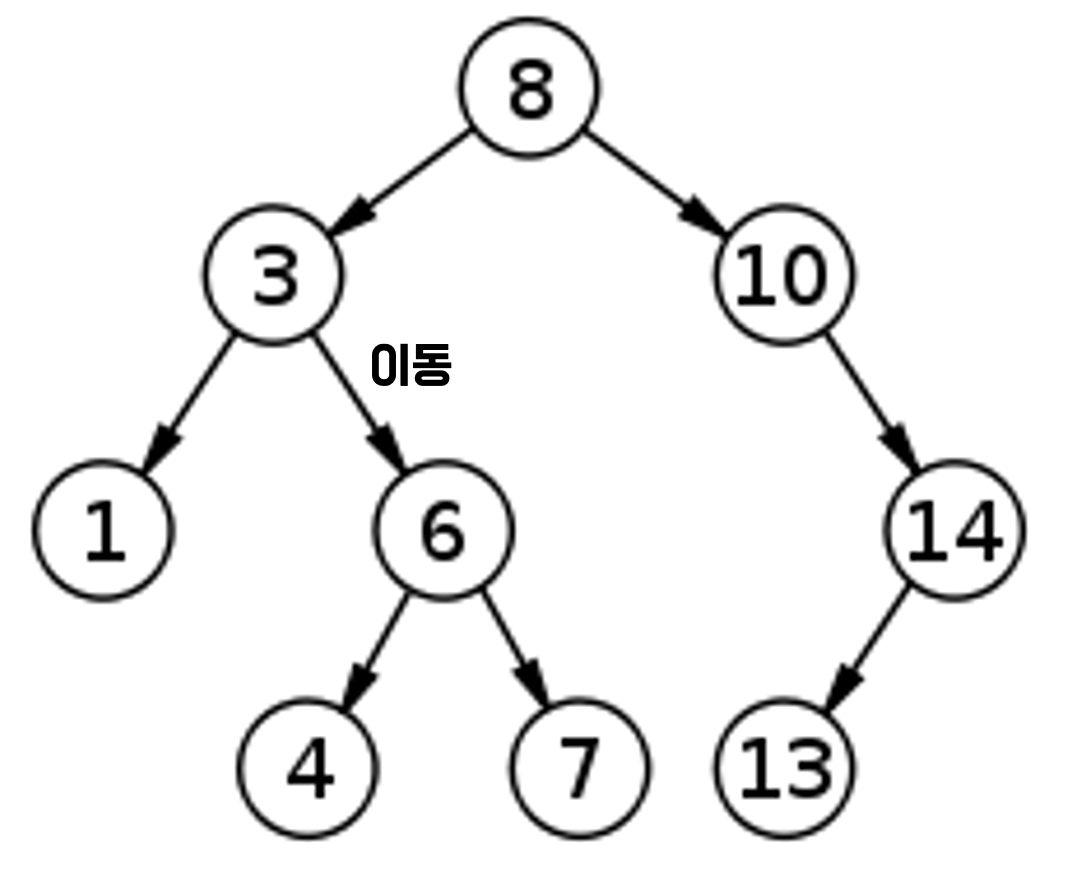
- 4는 3보다 크므로 오른쪽으로 이동한다.
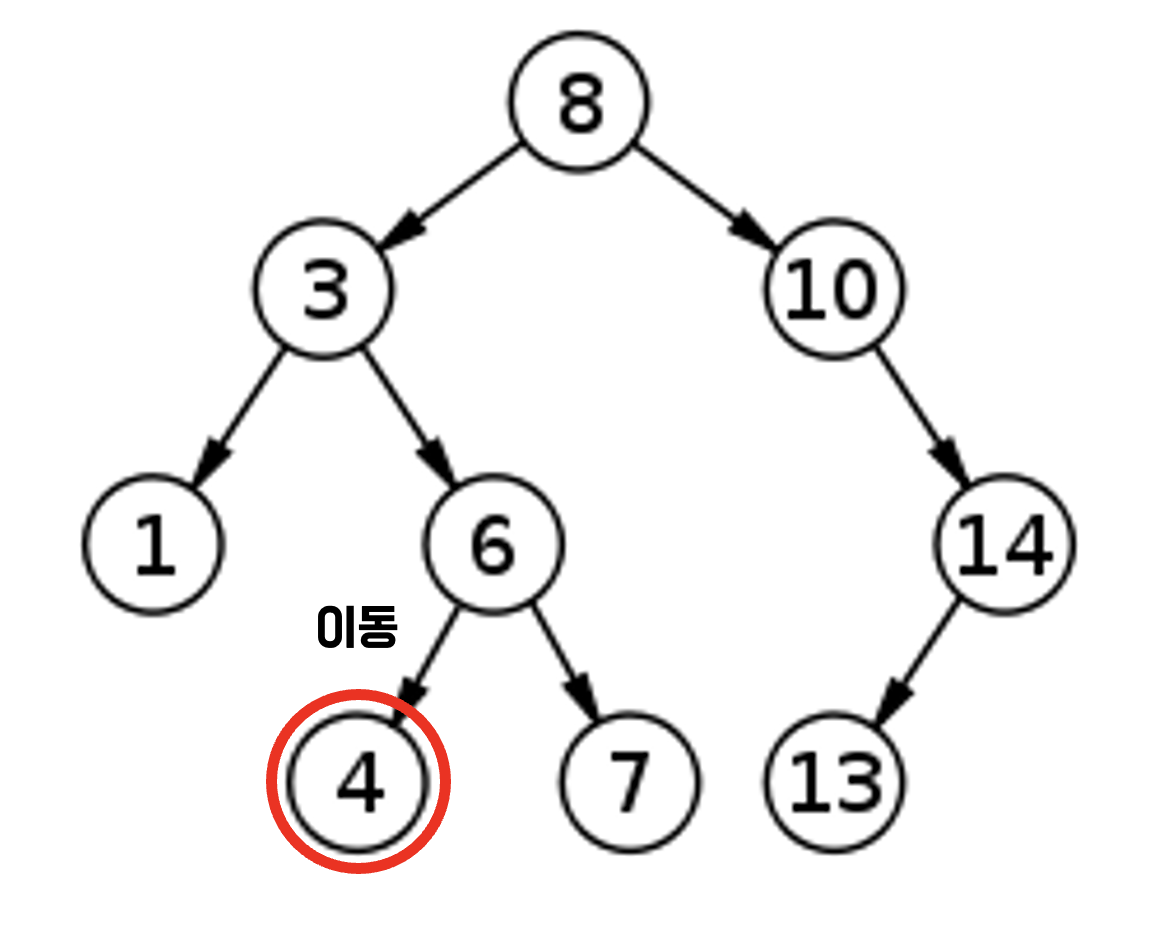
- 4는 6보다 작으므로 왼쪽으로 이동한다
- 4를 찾았다.
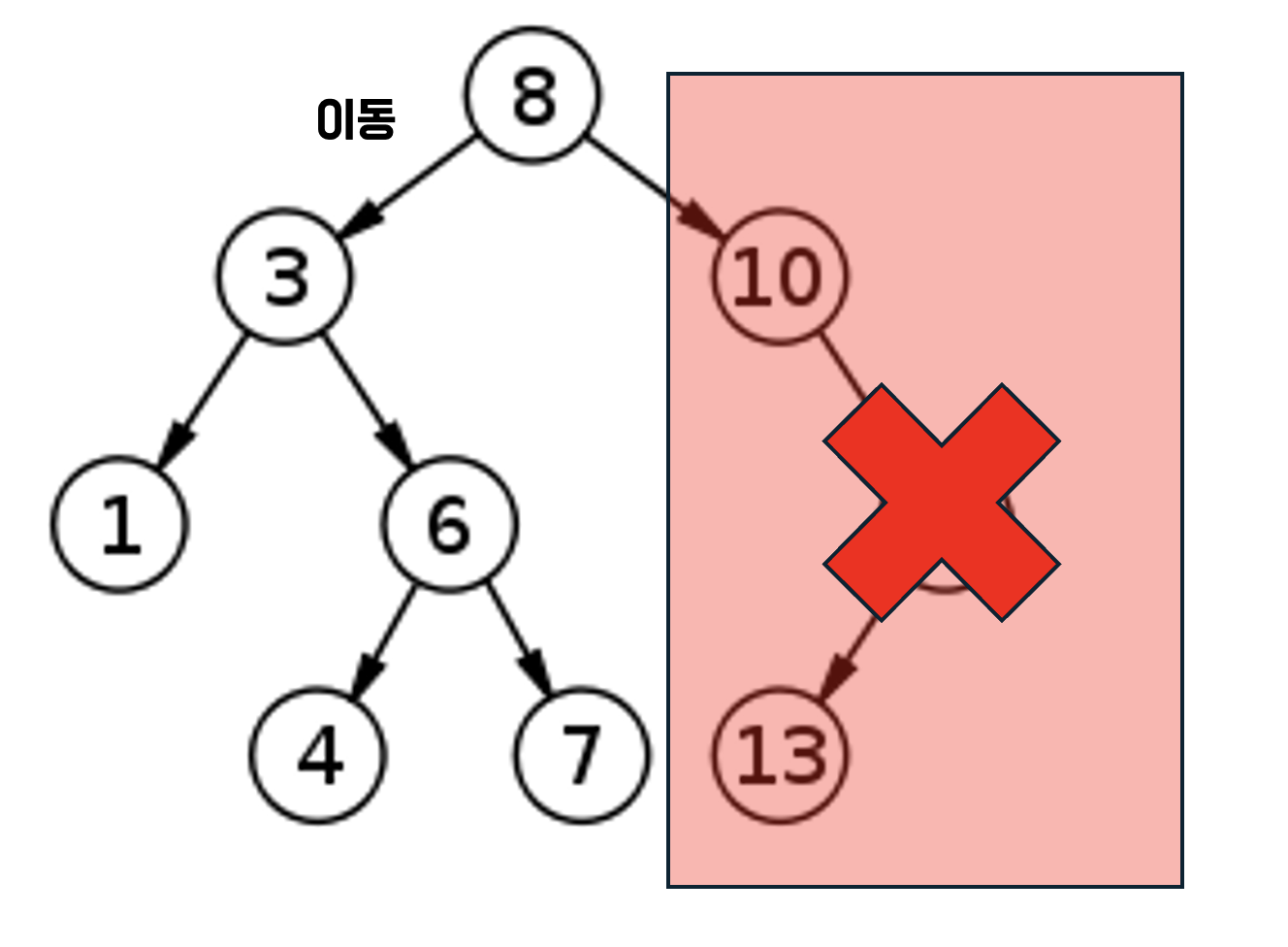
이진 탐색트리에서 특정 값을 탐색할 때 아래 노드로 내려갈 때마다 그 반대쪽 노드들은 무시해도 되게 된다.
이는 시간복잡도가 O(logN)이 됨을 의미한다.
배열에서는 인덱스 순서대로 비교해가며 탐색을 했기 때문에 O(N)으로 탐색을 해야했지만
트리에서는 O(logN)의 시간복잡도 만으로 탐색을 할 수 있다.
삭제
삭제하는 케이스를 나누면 크게 두 가지로 나눌 수 있다.
1. 리프 노드를 삭제하는 경우
2. 리프 노드가 아닌 노드를 삭제하는 경우
1. 리프 노드를 삭제하는 경우에는 간단하다. 그냥 삭제하면 된다.
예를 들어 4를 삭제하는 경우
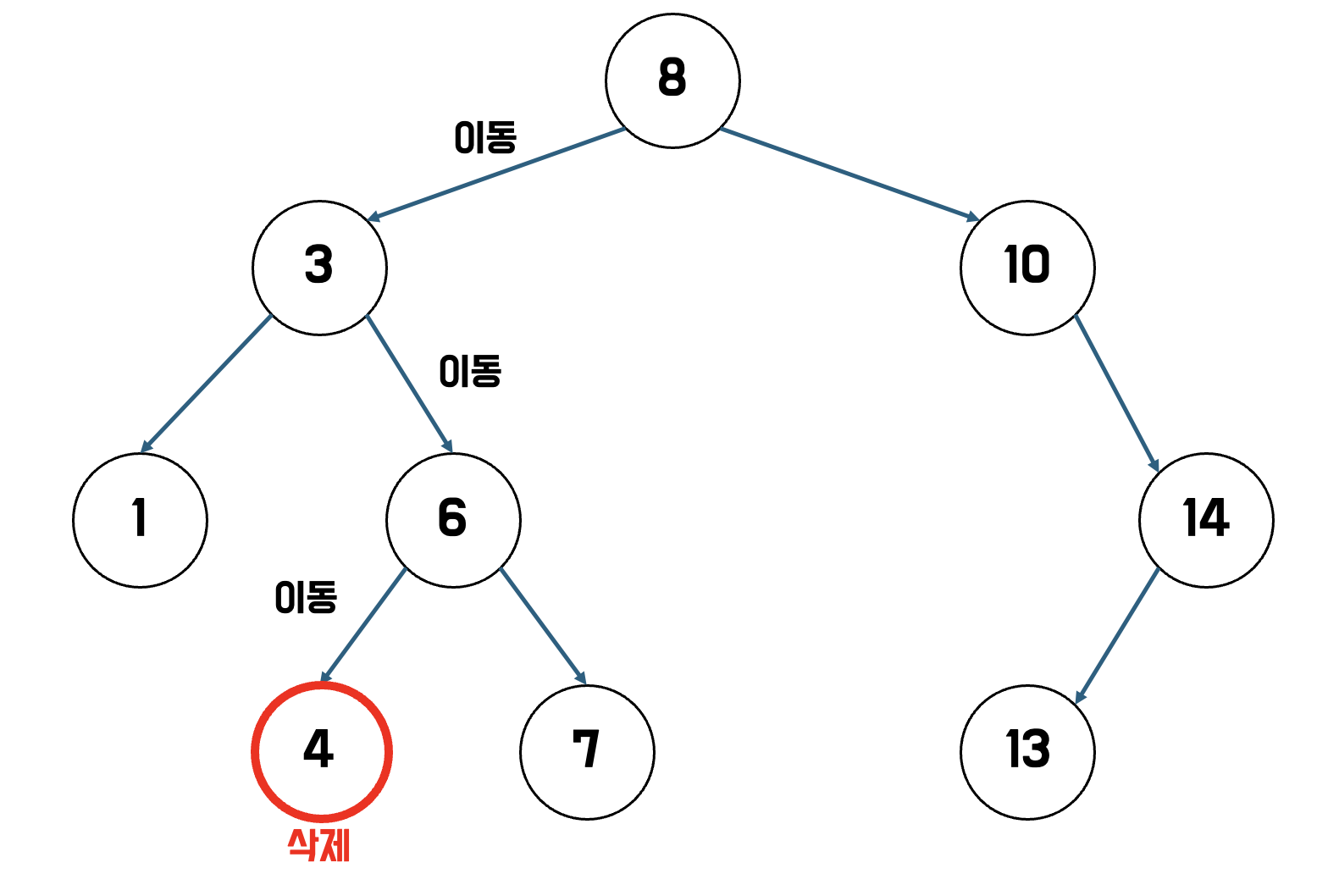
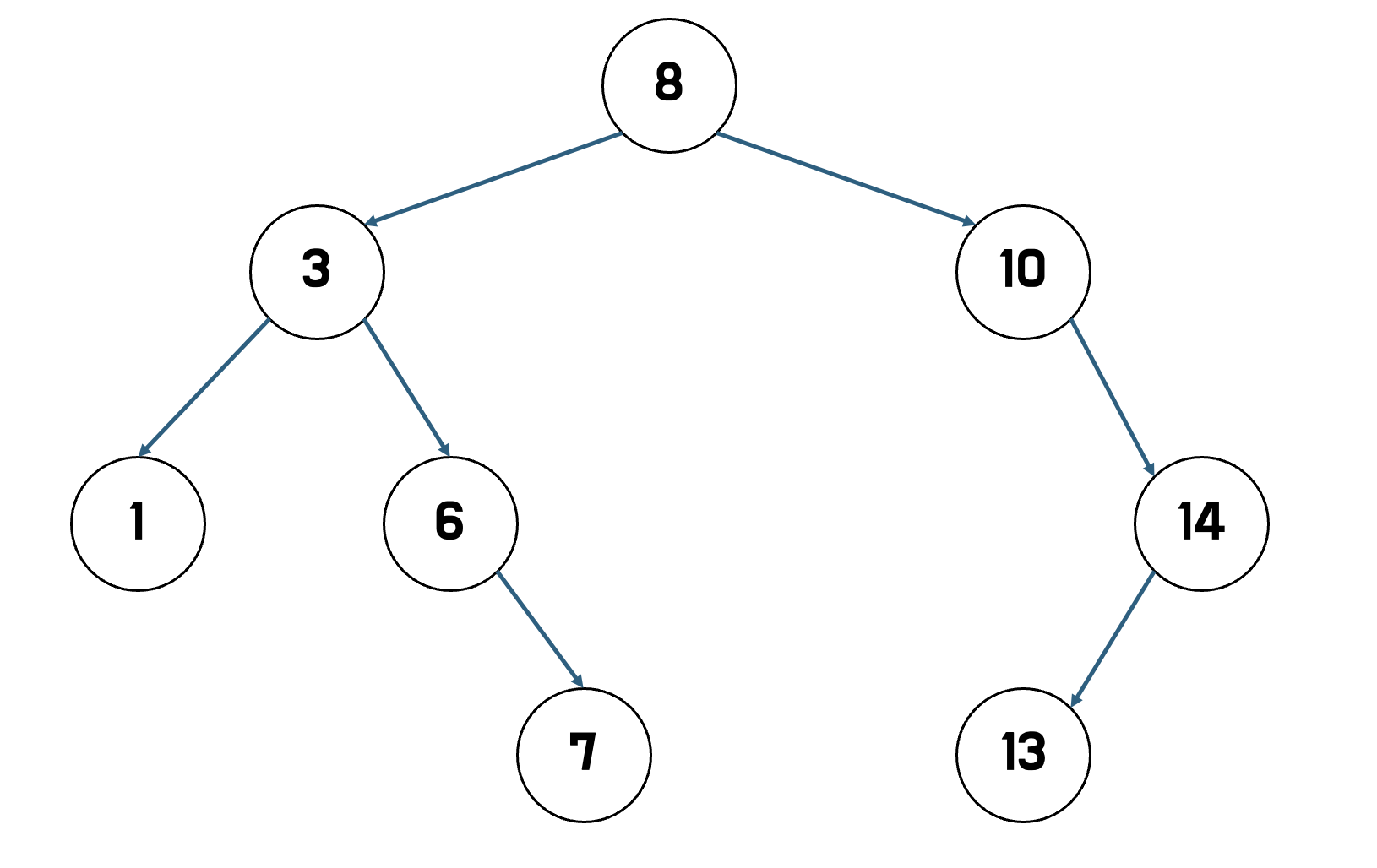
- 4를 찾아 삭제하면 된다.
문제는 2. 리프 노드가 아닌 노드를 삭제하는 경우이다. 리프노드가 아닌 노드를 삭제하게 되면 중간 연결다리가 끊기는 것이므로 재조립을 해줘야한다.
재조립하는 경우도 크게 두가지로 나눌 수 있다.
2-1. 자식 노드가 한 개인 경우
2-2. 자식 노드가 두 개인 경우
2-1. 자식 노드가 한 개인 경우부터 보겠다.
예를 들어 14를 삭제한다고 하자
1.


- 14를 찾아서 삭제한다.
2.
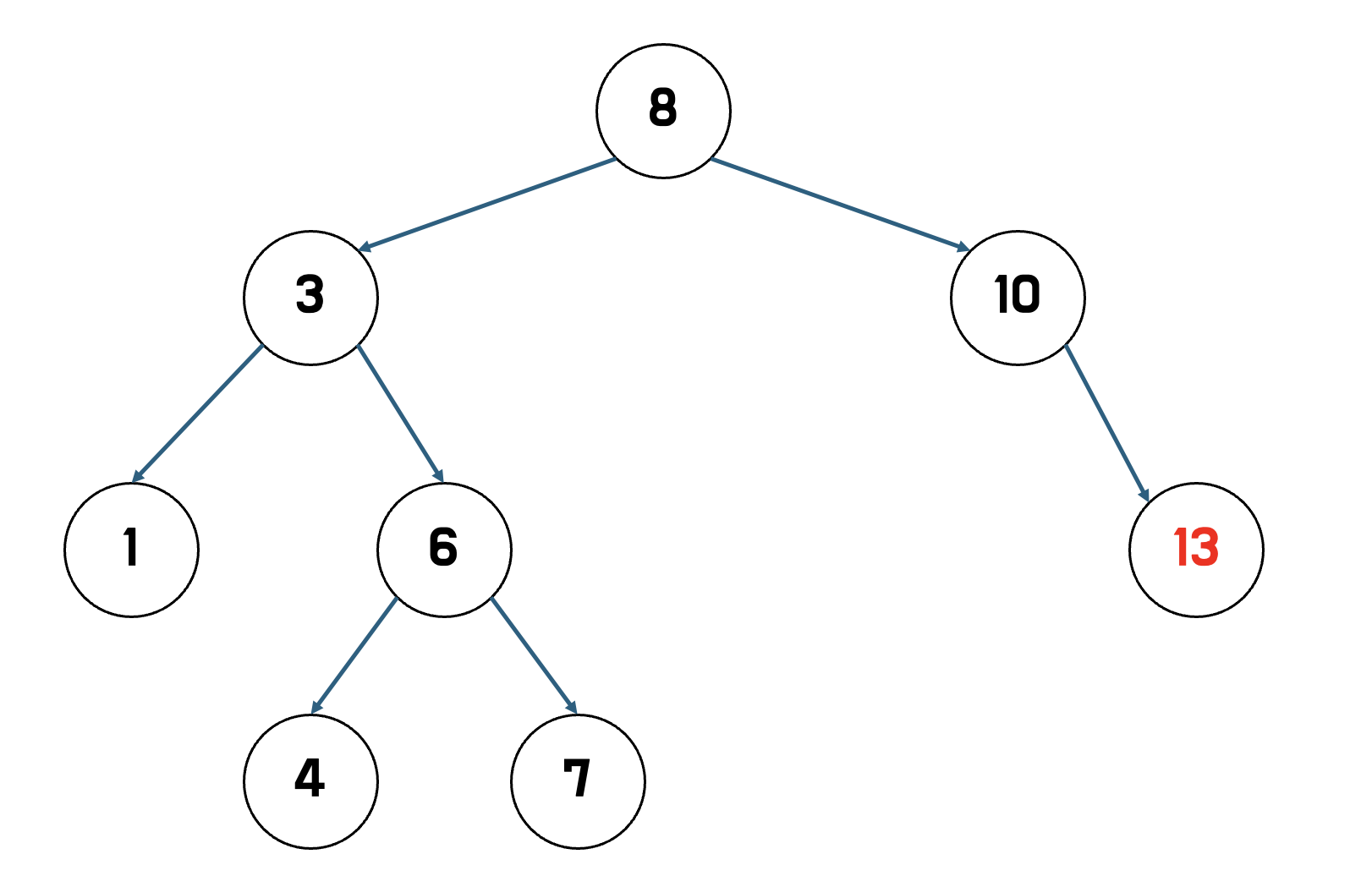
- 자식 노드를 삭제된 노드 자리에 넣는다.
다음은 2-2. 자식 노드가 두 개인 경우이다.
예를 들어 3을 삭제한다고 가정해보자.
1.

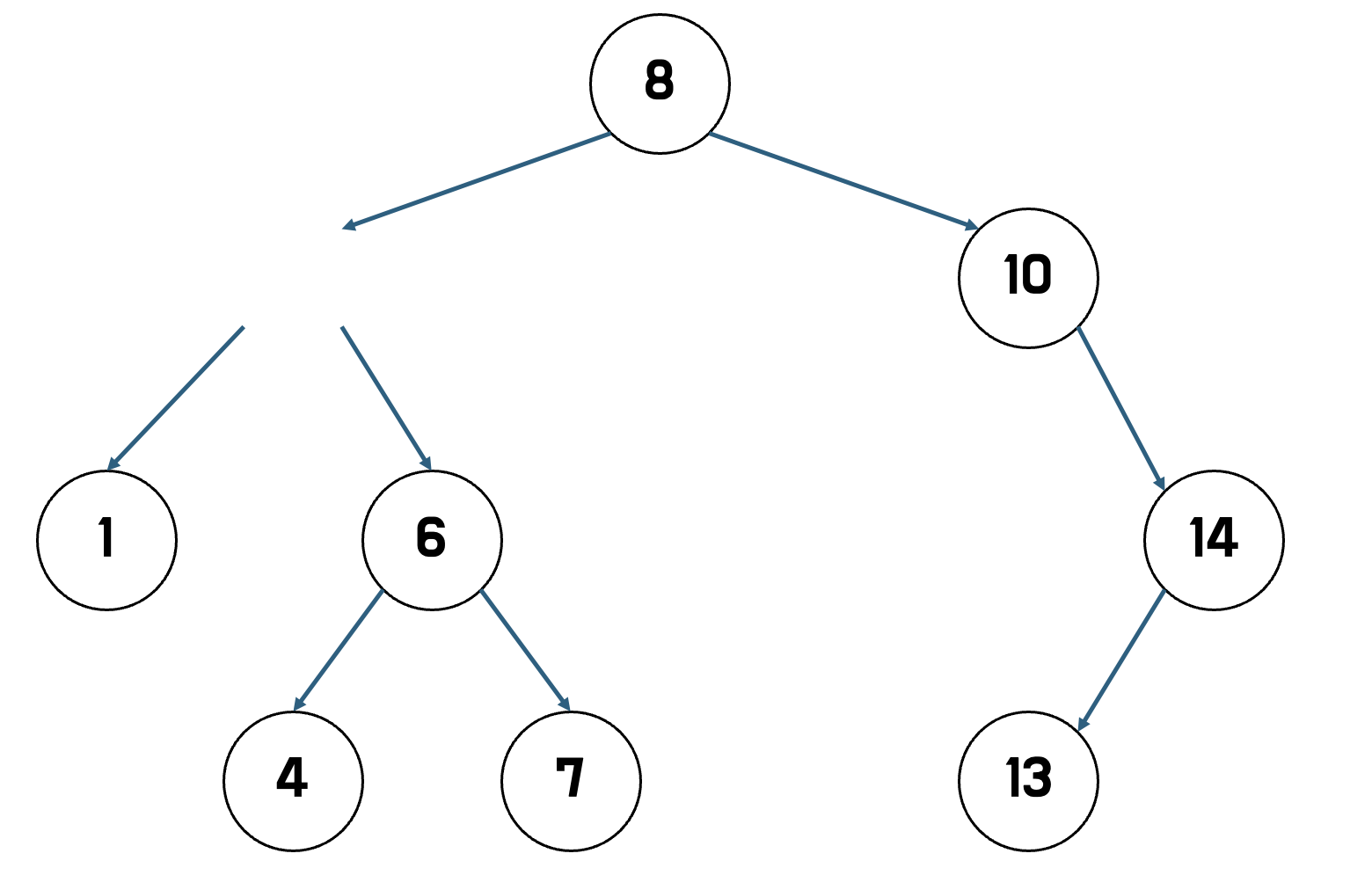
- 3을 찾아서 삭제한다.
2.
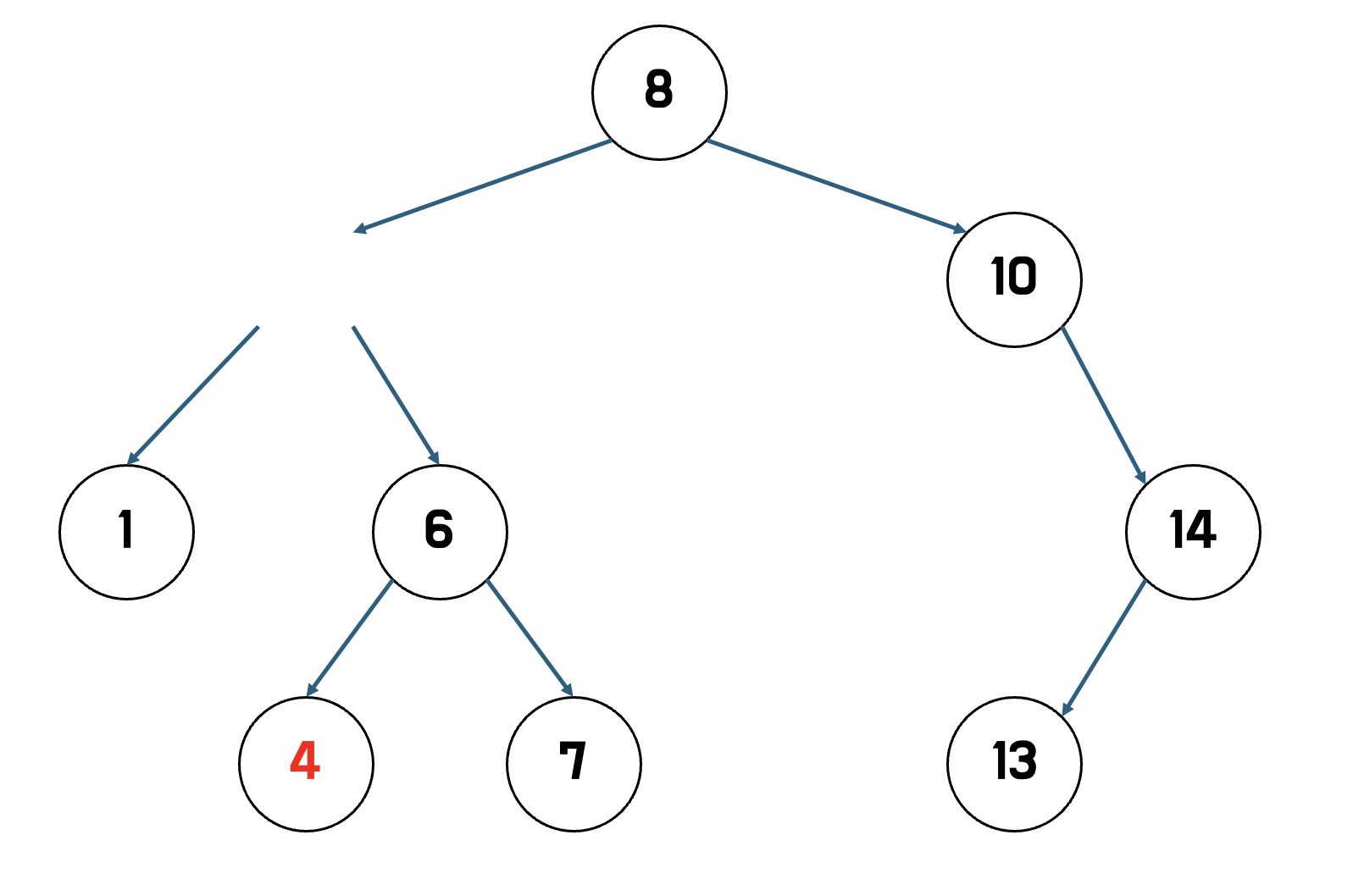
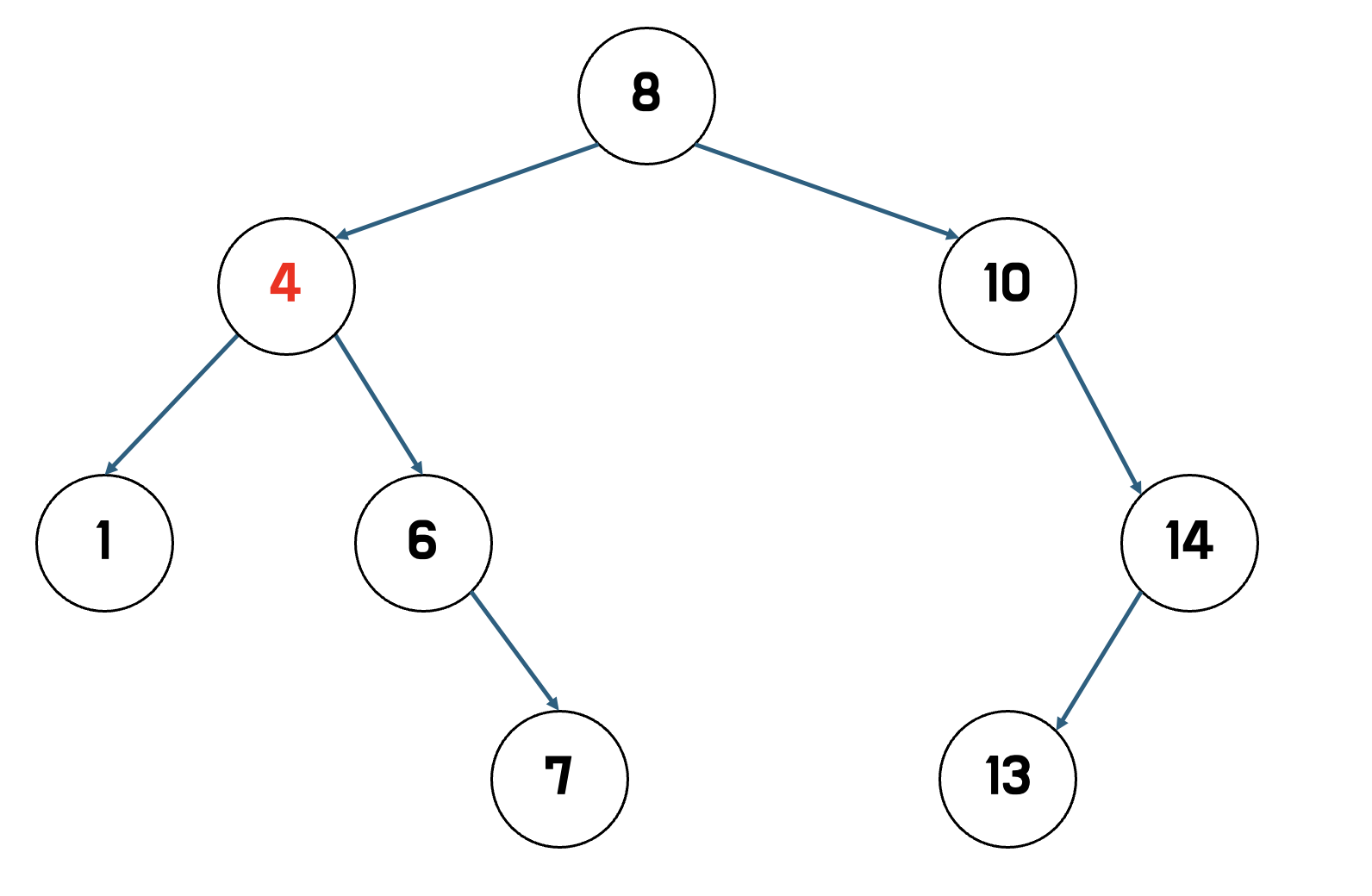
- 삭제된 노드의 오른쪽 노드 중 제일 작은 값을 찾아 삭제된 자리에 넣는다.
정리하면 다음과 같다.
1. 리프 노드를 삭제하는 경우
--> 그냥 삭제한다.
2. 리프 노드가 아닌 노드를 삭제하는 경우
2-1. 자식 노드가 한 개인 경우
--> 삭제하고 자식 노드를 그 자리에 넣는다.
2-2. 자식 노드가 두 개인 경우
---> 삭제하고 오른쪽 자식 노드중 가장 작은 노드를 그 자리에 넣는다.
이진 탐색 트리 표현하기

배열로 표현하기
1.

- 노드에 대해 각각 인덱스를 매긴다
- 루트노드 1
- 왼쪽 노드 2, 오른쪽 3 ...
- 이렇게 순서대로 숫자를 매기다보면 다음과 같은 규칙이 생긴다.
- 노드의 인덱스에 곱하기 2를 하면 왼쪽 노드의 인덱스가 나온다
- 노드의 인덱스에 곱하기 2 더하기 1을 하면 오른쪽 노드의 인덱스가 나온다.
실제 배열에 트리의 값을 저장하면 다음과 같다.

배열로 구현하면 매우 쉽게 트리를 구현할 수 있다.
하지만 이렇게 되면 배열 중간중간이 비어있게 된다. 즉, 메모리 낭비가 일어나게 된다.
포인터로 표현하기
포인터를 이용해서 자신의 왼쪽 자식노드, 오른쪽 자식노드에 대한 포인터 값을 저장하면 된다.
그림으로 표현하면 다음과 같다.

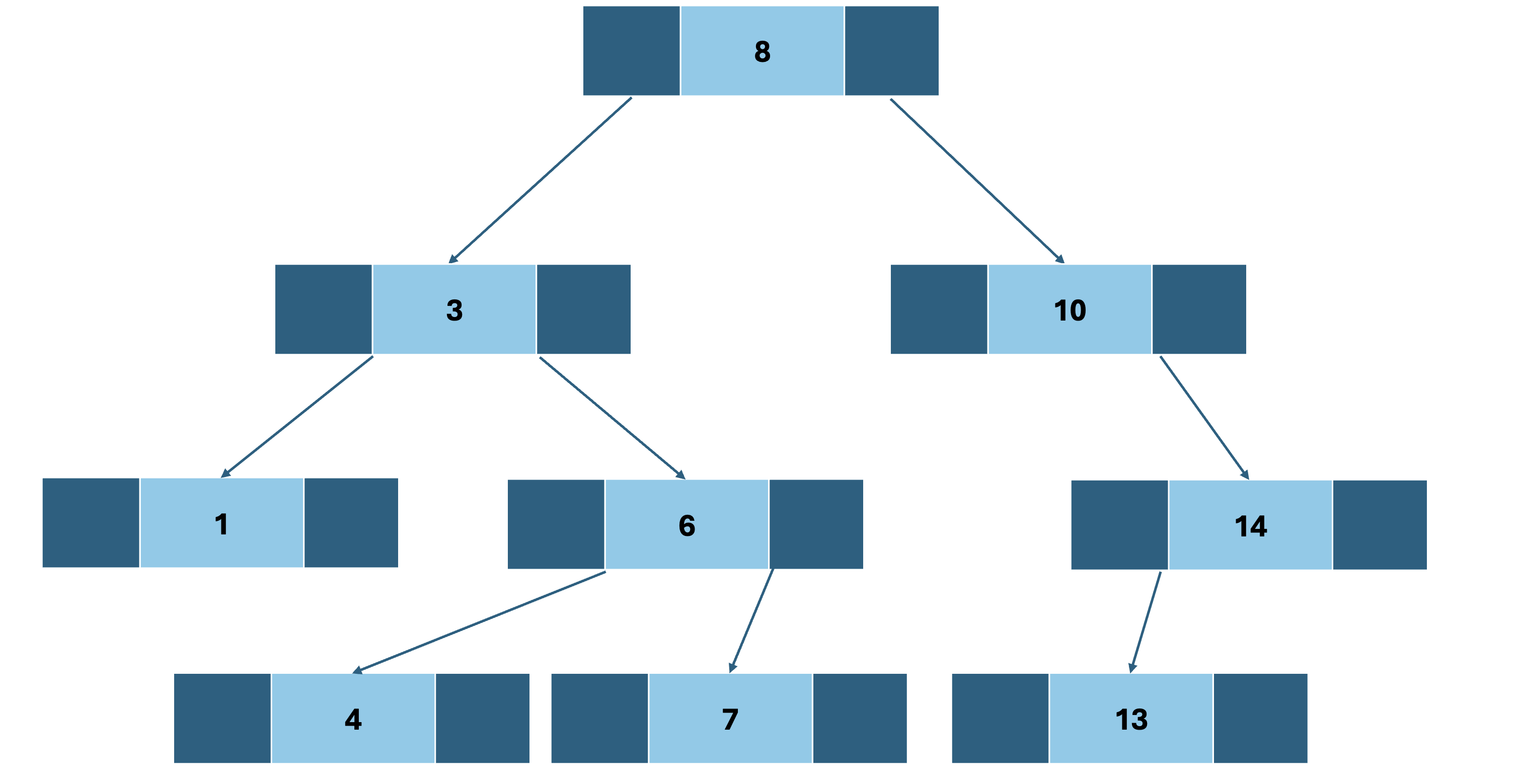
포인터로 트리를 표현하게 되면 메모리 낭비가 일어나지 않게 된다.
하지만 구현난이도가 올라간다.
인접 리스트로 표현하기
각 노드마다 리스트를 만들어서 해당 노드와 연결된 노드를 리스트에 저장한다.
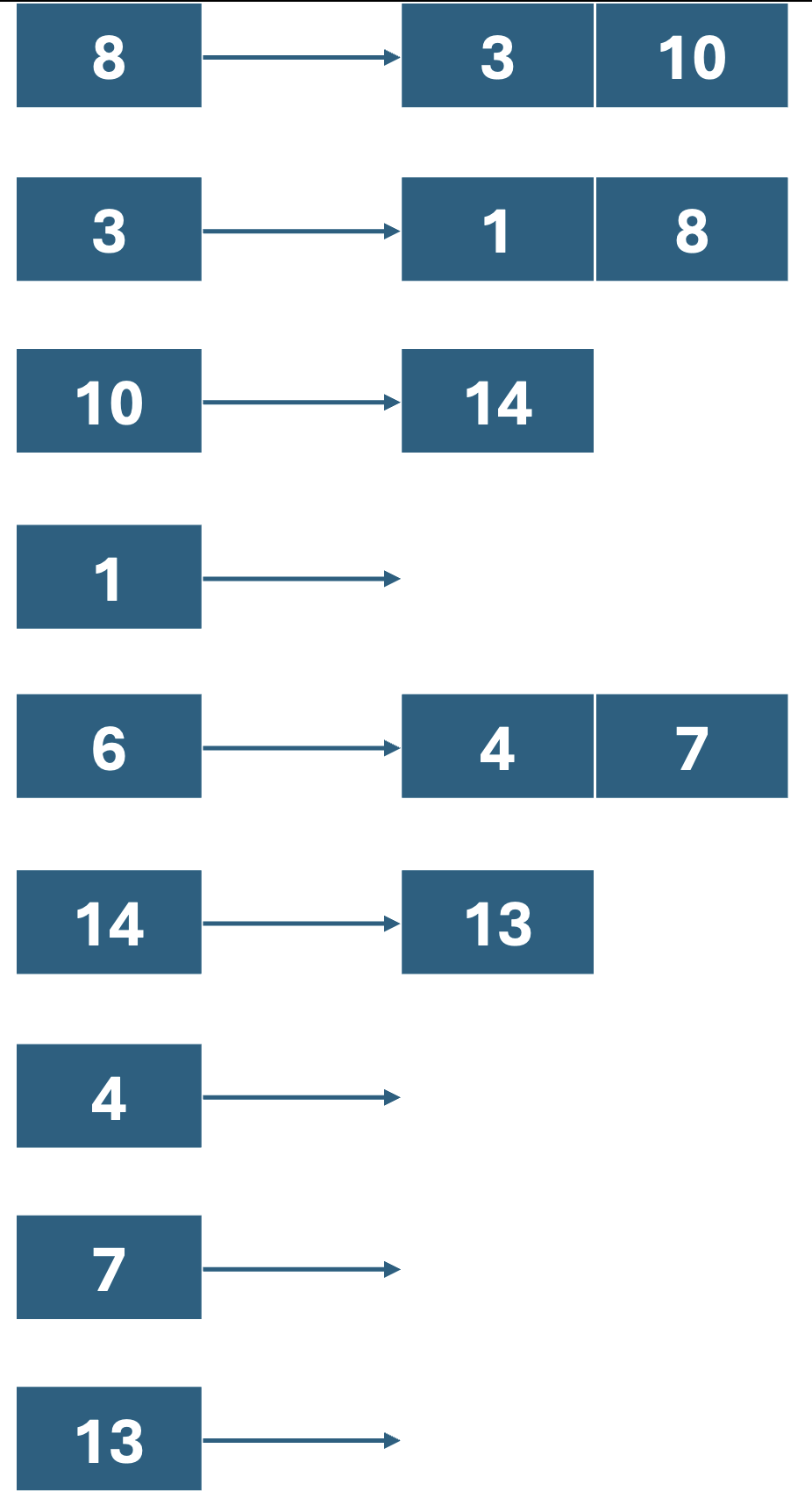
- 이렇게 하면 자식 노드의 수가 2개 이상일 경우도 표현하기 좋다
- 또한 메모리 공간이 낭비되지 않는다.
- 하지만 구현 난이도가 어렵다
해당 포스트는 『코딩 테스트 합격자 되기 - 자바편』을 참고하여 작성되었습니다.
'코딩 테스트 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 그래프 (Graph) (0) | 2024.05.29 |
|---|---|
| 상호베타적(서로소) 집합과 유니온 파인드 알고리즘 (0) | 2024.05.24 |
| 트리(Tree) (0) | 2024.05.21 |
| 해시 (Hash) (0) | 2024.05.06 |
| 큐(Queue) (0) | 2024.05.04 |
