그래프(Graph)란?
그래프(Graph)란 노드와 간선을 이용한 비선형 데이터 구조로 데이터 간의 관계를 표현하는데 사용된다.
데이터를 노드로 데이터 간의 관계는 간선으로 표현한다.
또한 데이터 간의 관계에서 정도를 표현할 필요가 있다면 가중치를 사용해 표현한다.
그림으로 표현하면 다음과 같다.
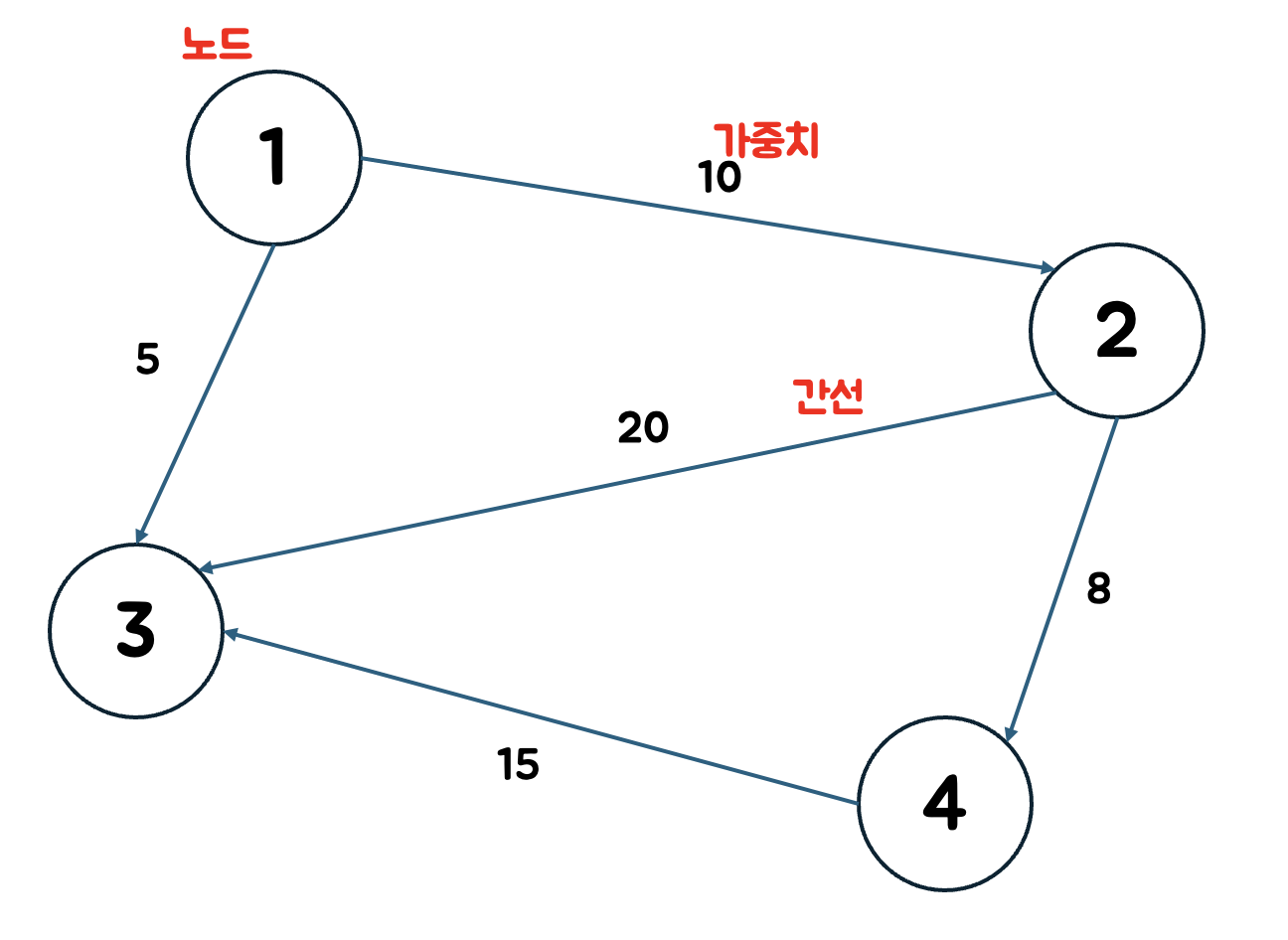
참고로 노드, 간선, 가중치는 다음과 같은 용어로 혼용된다.
- 노드(Node)
- 정점
- 버텍스(vertex)
- 간선
- 엣지(Edge)
- 가중치(Weight)
- 비용(cost)
그래프의 종류
방향성
간선은 그래프에서 두 정점간의 관계를 나타낸다.
그래프에서 간선은 방향을 가질 수도 있고 없을 수도 있다.
그래프가 방향이 있는 간선을 포함하면 방향 그래프
그래프가 방향이 없는 간선을 포함하면 무방향 그래프라고 한다.
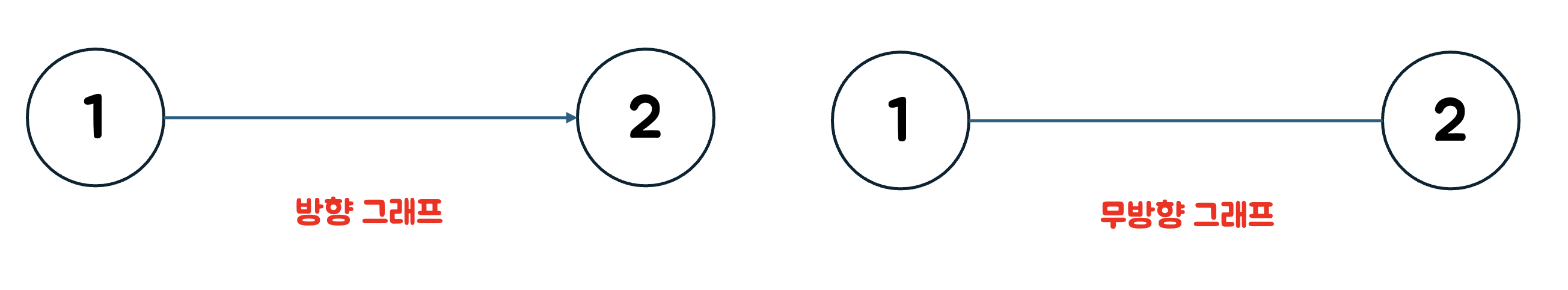
가중치
그래프에선 가중치를 통해 관계의 정도를 표현한다.
가중치가 있는 그래프를 가중치 그래프라고 한다.

순환
순환이란 한 정점에서 시작해서 다시 그 정점으로 돌아오는 구조를 의미한다.
순환이 존재하는 그래프를 순환 그래프(cycle graph)
순환이 존재하지 않는 그래프를 비순환 그래프(acyclic graph)라고 한다.
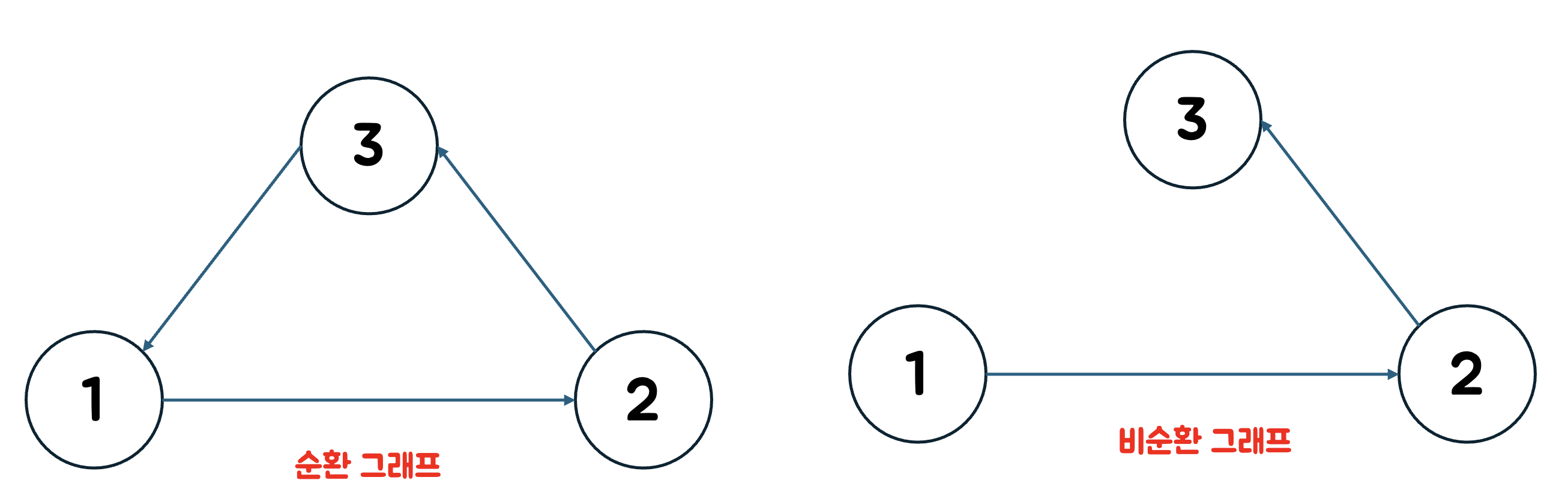
한가지 주의해야할 점이 있다.
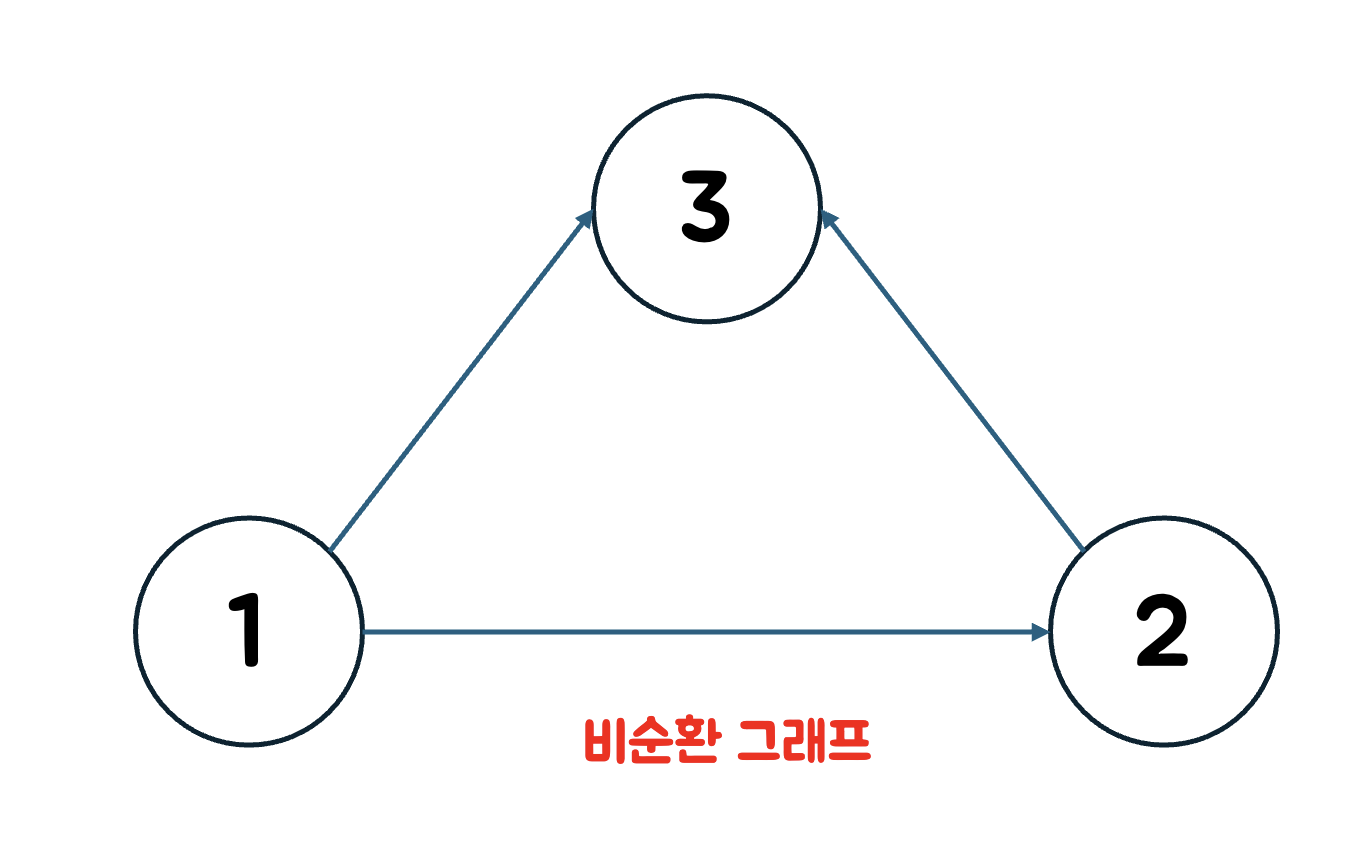
위의 그래프는 언뜻보면 순환그래프처럼도 보이지만 그래프 간선의 방향을 잘보면 한 노드에서 한노드로 돌아오는 부분이 존재하지 않는다.
따라서 비순환 그래프이다.
이렇듯 순환여부를 따질 때는 간선의 방향도 유의깊게 봐야한다.
그래프 구현하기
그래프를 구현하는 방법에는 크게 두 가지가 있다.
1. 인접행렬
첫 번째는 인접행렬로 구현하는 것이다.
인접행렬은 2차원배열로 쉽게 구현할 수 있다.
행을 출발 노드로 열을 도착 노드로 설정한다.
즉, 0번 노드에서 1번노드로 향하는 간선의 가중치가 10인 경우
arr[0][1] = 10이 된다.

예시 코드를 보도록하자
public static class Graph_matrix {
int[][] adjacent;
int V;
Graph_matrix (int V) {
adjacent = new int[V][V];
}
public void addEdge(int src, int dest, int weight) {
adjacent[src][dest] = weight;
}
}V는 노드의 갯수이다.
행렬은 노드의 갯수 X 노드의 갯수 만큼 있어야 한다.
단, 노드의 값이 0부터 순차적으로 늘어나는 경우에 한한다.
2. 인접 리스트
두 번째는 인접 리스트로 구현하는 것이다.
인접 리스트를 구현하기 위해선 노드를 적절히 정의해야한다.
노드는 도착 노드와 가중치로 이루어져 있다.

그런 다음 그래프 정점의 갯수 만큼 리스트를 준비한다.
이 리스트의 인덱스는 시작 노드를 의미한다.
그리고 각 리스트에 노드 리스트를 연결한다.
그림으로 보도록하자.
1. 그래프 정점의 갯수 만큼 리스트를 준비한다.

그래프의 정점이 4개이므로 4 크기의 리스트를 준비했다.
2. 각 리스트에 노드 리스트를 연결한다.
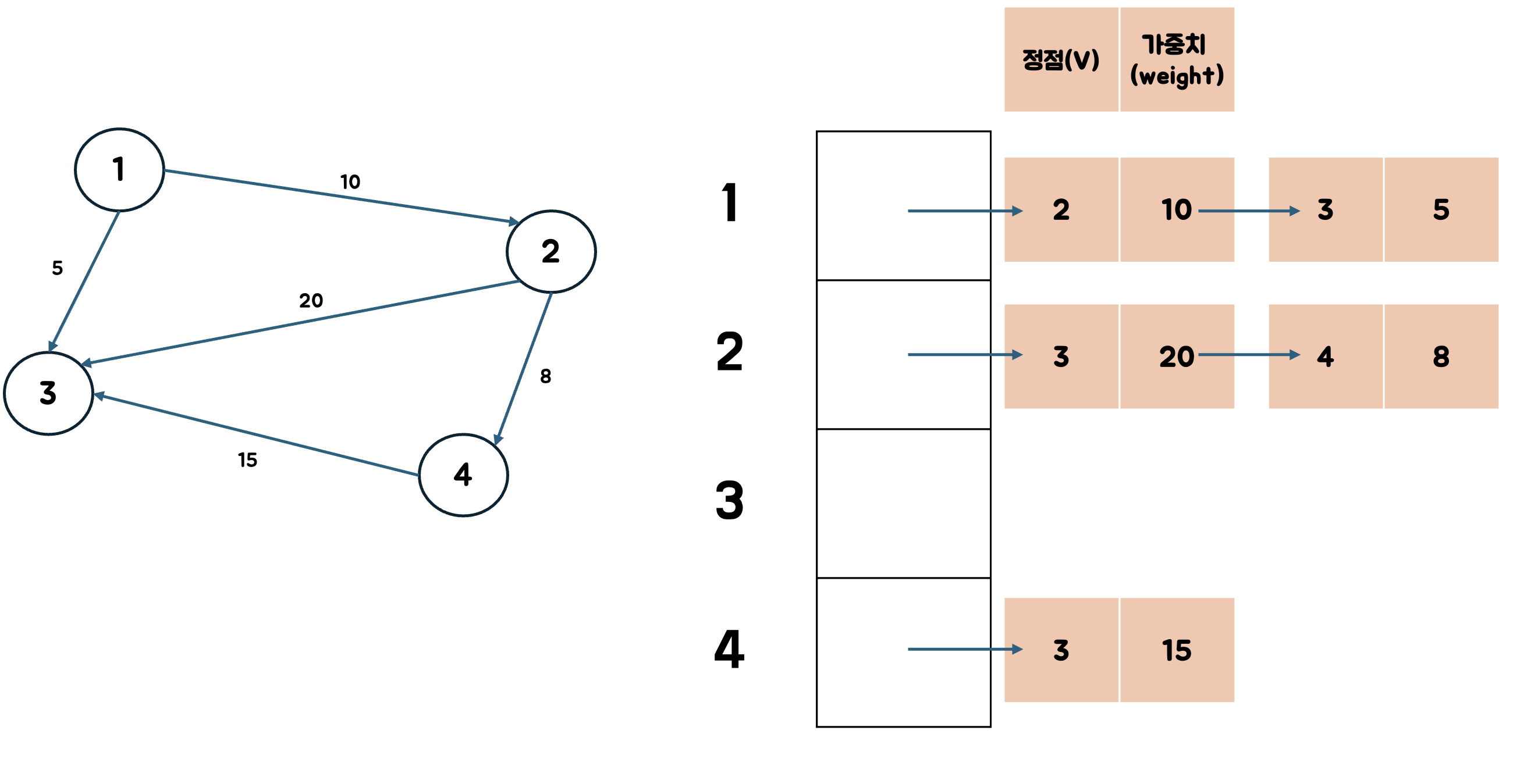
코드를 보도록하자
public static class Node {
int V;
int weight;
}
public static class Graph_list {
List<List<Node>> adjacent;
int V;
Graph_list (int V) {
adjacent = new ArrayList<>();
for(int i = 0; i < V; i++) {
adjacent.add(new ArrayList<>());
}
}
public void addEdge(int src, Node node) {
adjacent.get(src).add(node);
}
}Node를 별도의 클래스로 구현하였고
그래프는 ArrayList안에 Node에 대한 ArrayList를 정의하였다.
3. 인접 행렬 VS 인접 리스트
| E: 간선의 수 V: 정점의 수 |
메모리 사용 | 시간 복잡도 (A->B로 연결된 간선을 찾을 때) |
시간복잡도 (모든 정점에 대해서 연결된 간선을 찾을 때) |
| 인접 행렬 | O(E^2) | O(1) | O(E^2) |
| 인접 리스트 | O(E + V) | O(E) (모든 간선이 하나의 정점에만 연결되어 있는 경우에만) (평균적으로는 O(E/V) |
O(V + E) |
특정 노드에서 특정 노드로 연결된 간선을 찾는 경우를 제외하고는 인접리스트가 효율이 좋다.
보통 그래프를 가지고 문제를 푸는 경우 한 간선만 찾는 경우는 거의 없으므로 코딩테스트에서는 인접리스트를 사용해서 구현하는 편이다.
또한 표 내용 말고도 인접행렬보다 인접리스트가 좋은 이유가 한가지가 있는데
일단 이 표는 모든 정점의 데이터가 0부터 순차적으로 증가하는 경우(배열의 인덱스와 유사한 형태)를 가정한다.
하지만 정점의 데이터가 순차적으로 증가하는 것이 아닌 0, 1, 2, 3, 999처럼 불규칙적이라면 어떻게 될까?
이렇게 되면 인접행렬의 경우 행렬의 크기를 정점의 수 X 정점의 수로 해야하는 것이 아니라
정점의 최대크기 X 정점의 최대 크기로 해야한다. 즉, 위의 예시의 경우 999 X 999가 돼야 한다.
메모리 낭비가 상당히 일어난다.
반면 인접 리스트의 경우엔 어떨까?
물론, 인접 리스트를 다음 방식처럼 구현하면 인접행렬과 다를바가 없다.
public static class Node {
int V;
int weight;
}
public static class Graph_list {
List<List<Node>> adjacent;
int V;
Graph_list (int V) {
adjacent = new ArrayList<>();
for(int i = 0; i < V; i++) {
adjacent.add(new ArrayList<>());
}
}
public void addEdge(int src, Node node) {
adjacent.get(src).add(node);
}
}이 코드도 결국 정점 갯수만큼 리스트를 만든 것이라서 출발 노드가 인덱스가 된다.
즉, 인접행렬과 다를바가 없다.
하지만 이를 리스트가 아니라 해시맵으로 바꾼다면 이야기가 달라진다.
public static class Node {
int V;
int weight;
}
public static class Graph_list {
HashMap<Integer, List<Node>> adjacent;
// 그래프 생성자
public Graph_list() {
adjacent = new HashMap<>();
}
// 간선 추가
public void addEdge(int src, Node node) {
adjacent.putIfAbsent(src, new ArrayList<>());
adjacent.putIfAbsent(dest, new ArrayList<>());
adjacent.get(src).add(node);
}
}간선을 추가할 때마다 없는 정점을 동적으로 추가하는식으로 구현하면 아무리 정점의 데이터가 불규칙적이라도 문제없이 해결할 수 있다.
지금까지 그래프의 기본적인 개념과 구현방식에 대해 알아봤다.
'코딩 테스트 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 그래프 최단 경로 알고리즘 - 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2024.05.31 |
|---|---|
| 그래프의 탐색(깊이 우선 탐색과 너비 우선탐색) (0) | 2024.05.29 |
| 상호베타적(서로소) 집합과 유니온 파인드 알고리즘 (0) | 2024.05.24 |
| 이진 탐색 트리(Binary Search Tree) (0) | 2024.05.21 |
| 트리(Tree) (0) | 2024.05.21 |
