다익스트라 알고리즘(Dijkstra Algorithm)이란?

다익스트라 알고리즘이란 에츠허르 다익스트라가 제안한 최단 거리 알고리즘이다.
다익스트라 알고리즘은 위와 같이 가중치가 존재하는 그래프에서 특정 노드에서 다른 노드까지의 최단경로 및 최단거리(최소비용)를 구할 때 사용된다.
다익스트라 알고리즘 동작 방식
다익스트라 동작방식은 다음과 같다.
1. 시작 노드를 정하고 테이블을 초기화한다. 테이블에는 시작 노드에서 각 노드까지의 최소 비용과 직전 노드를 저장한다.
1-1. 시작 노드의 경우 최소 비용을 0, 직전 노드를 자기 자신으로 초기화 한다.
1-2. 나머지 노드의 경우 최소 비용을 무수히 큰 값, 직전 노드를 임의의 더미 값으로 초기화한다.
2. 다음을 수행한다.
2-1. 방문하지 않는 노드들 중 비용이 가장 적은 노드부터 현재 노드로 설정하여 수행한다.
(시작 노드는 0으로 초기화하였으므로 무조건 시작 노드가 최초 방문 노드)
2-2. 현재 노드와 방문하지 않은 인접 노드 간의 가중치를 통해 현재 노드를 거쳐 인접한 노드로 가는 비용과
기존의 테이블에 저장되어있던 최소비용을 비교하여 전자가 더 작은 경우 테이블의 최소 비용을 해당 값으로
업데이트한다. 직전 노드 값의 경우 현재 노드로 업데이트 한다.
3. 2의 과정을 노드 갯수 만큼 수행한다.
이렇듯 다익스트라 알고리즘은 그 순간 최소 비용을 가지는 노드를 방문하며 한번 방문한 노드는 다시 방문하지 않는다. 또한 현재 노드의 인접노드 중 방문한 노드도 무시한다.
이말을 다르게 말하면 한번 방문하면 그 방문노드까지의 최단 경로는 확정이 된다는 의미이다.
그림을 통해 보도록하자.
다음과 같은 그래프가 있다.

1. 시작 노드를 정하고 테이블을 초기화한다. 테이블에는 시작 노드에서 각 노드까지의 최소 비용과 직전 노드를 저장한다.
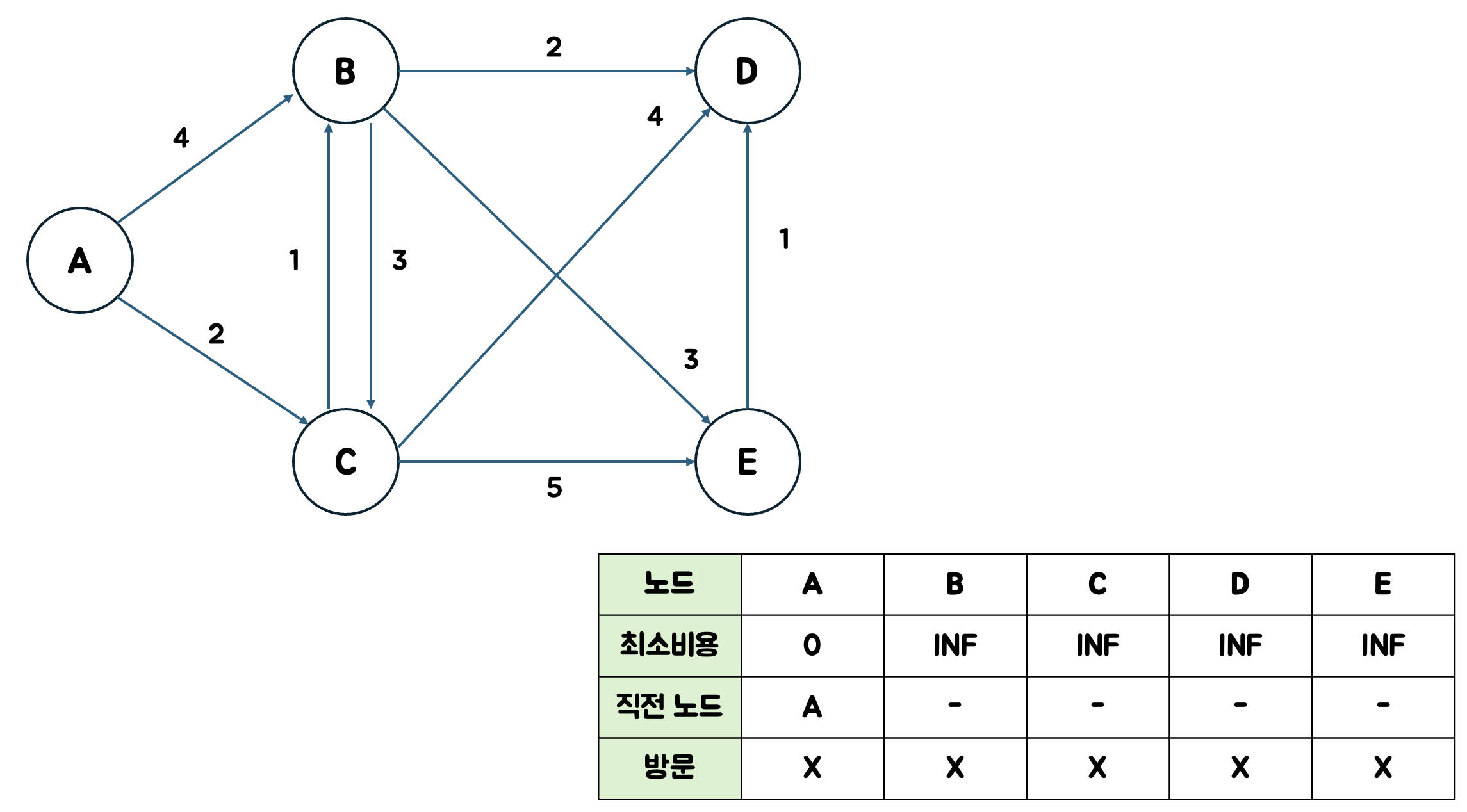
시작 노드는 A로 하였다.
1번째 반복
2-1. 방문하지 않는 노드들 중 비용이 가장 적은 노드부터 현재 노드로 설정하여 수행한다.

A가 0으로 비용이 제일 적으므로 A를 현재 노드로 하고 방문처리한다.
A까지의 최소비용은 0이고 최단 경로는 A가 된다.
2-2. 현재 노드와 방문하지 않은 인접 노드 간의 가중치를 통해 현재 노드를 거쳐 인접한 노드로 가는 비용과
기존의 테이블에 저장되어있던 최소비용을 비교하여 전자가 더 작은 경우 테이블의 최소 비용을 해당 값으로
업데이트한다. 직전 노드 값의 경우 현재 노드로 업데이트 한다.

- B의 경우 A를 거치면 4(0+4)이고 기존 테이블 비용은 INF이므로 테이블을 업데이트 한다.
직전 노드는 A로 업데이트 한다. - C의 경우 A를 거치면 2(0+2)이고 기존 테이블 비용은 INF이므로 테이블을 업데이트 한다.
직전 노드는 A로 업데이트 한다.
3. 2의 과정을 노드 갯수 만큼 수행한다.
2번째 반복
2-1. 방문하지 않는 노드들 중 비용이 가장 적은 노드부터 현재 노드로 설정하여 수행한다.

C가 비용이 제일 작으므로 C를 현재 노드로 하고 방문처리한다.
C까지의 최소 비용은 2이고 최단 경로는 A-C이다.
2-2. 현재 노드와 방문하지 않은 인접 노드 간의 가중치를 통해 현재 노드를 거쳐 인접한 노드로 가는 비용과
기존의 테이블에 저장되어있던 최소비용을 비교하여 전자가 더 작은 경우 테이블의 최소 비용을 해당 값으로
업데이트한다. 직전 노드 값의 경우 현재 노드로 업데이트 한다.
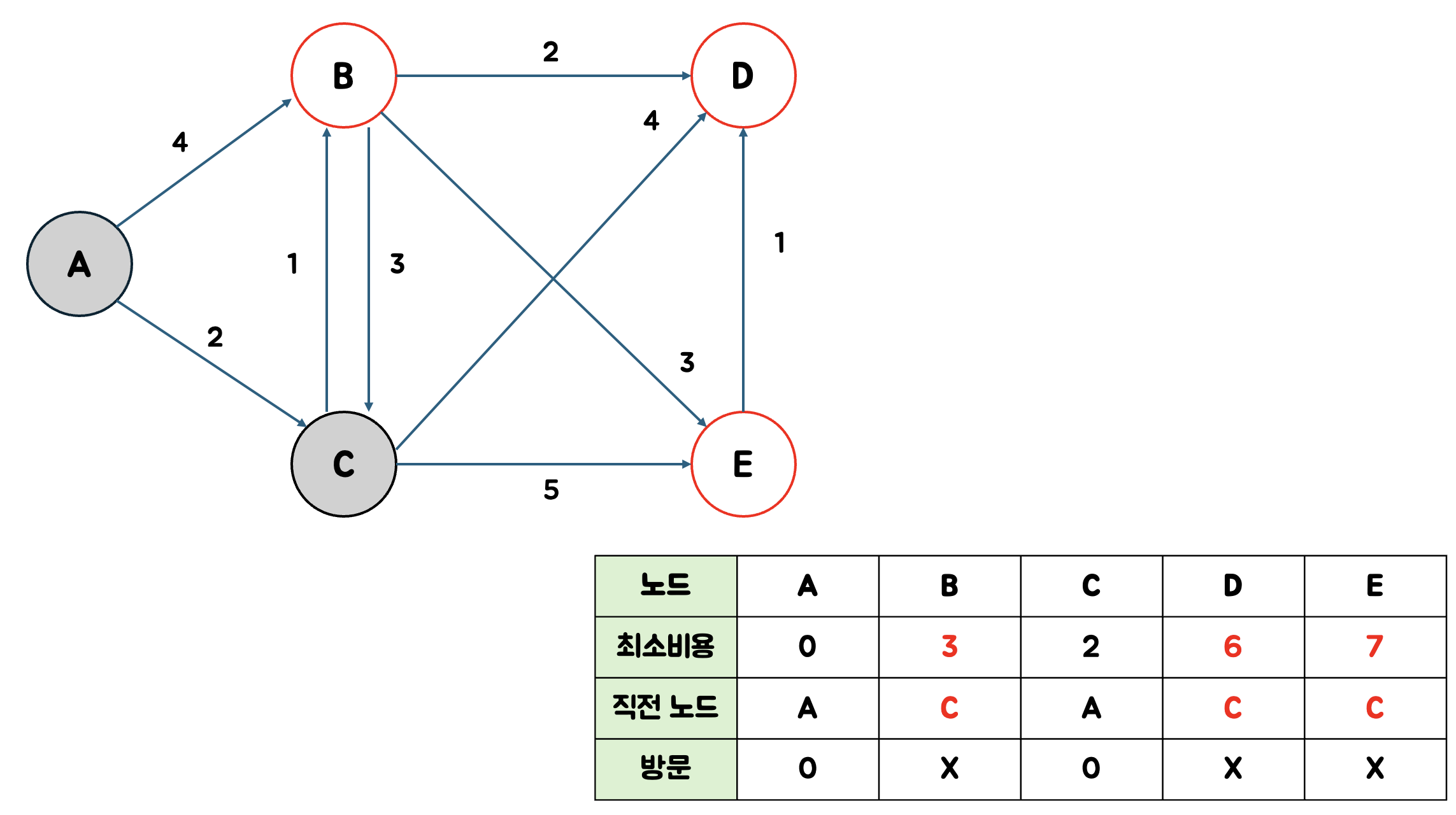
- B의 경우 C를 거치면 3(2+1)이고 기존 테이블의 값은 4였으므로 테이블을 3으로 업데이트 한다.
직전 노드는 C로 업데이트 한다. - D의 경우 C를 거치면 6(2+4)이고 기존 테이블의 값은
- E의 경우 C를 거치면 7(2+5)이고 기존 테이블의 값은 INF였으므로 테이블을 7로 업데이트 한다.
3번째 반복
2-1. 방문하지 않는 노드들 중 비용이 가장 적은 노드부터 현재 노드로 설정하여 수행한다.
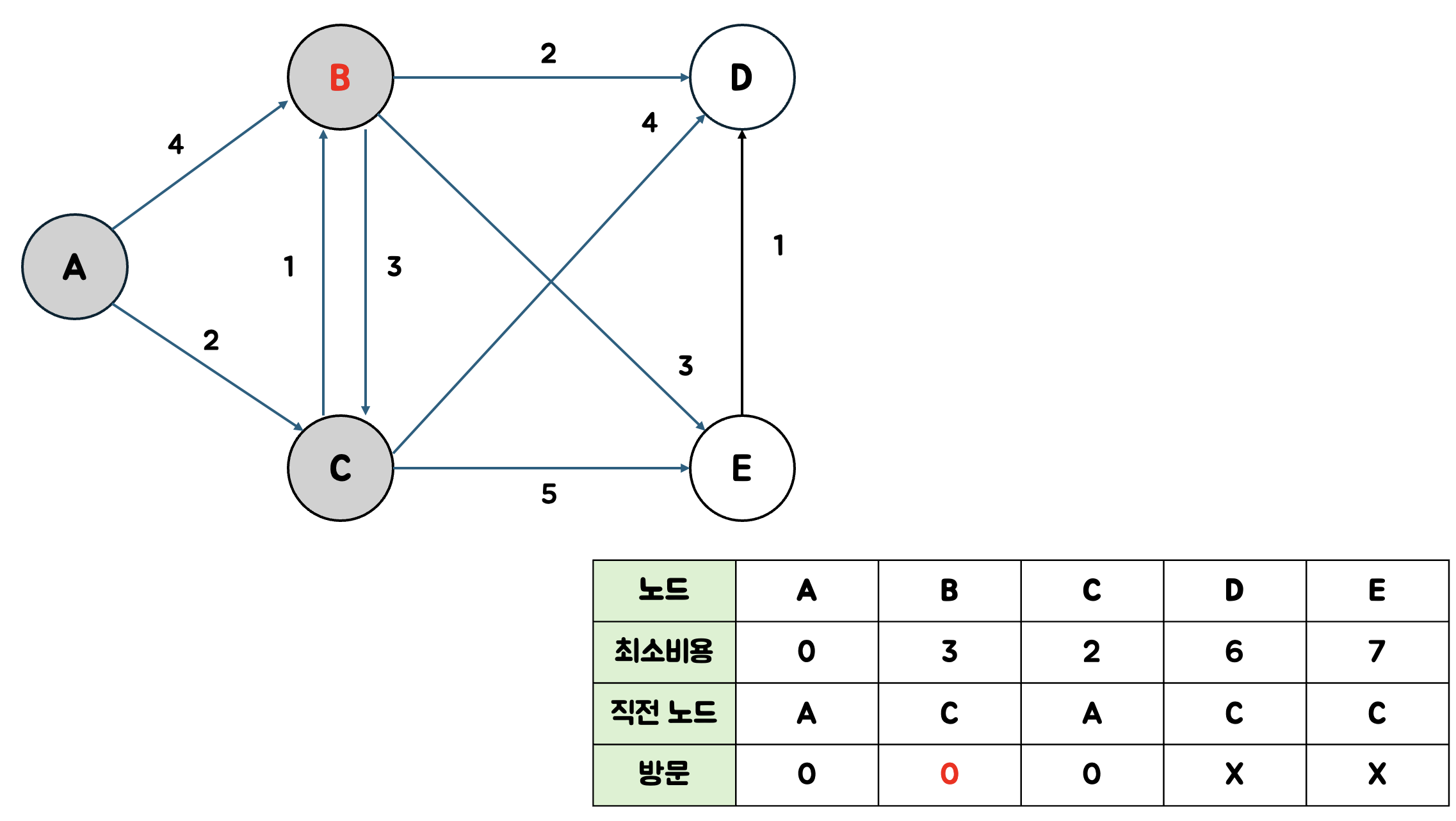
B가 비용이 제일 적으므로 B를 현재노드로 하고 방문처리한다.
B까지의 최소 비용은 3이고 경로는 A-C-B이다.
2-2. 현재 노드와 방문하지 않은 인접 노드 간의 가중치를 통해 현재 노드를 거쳐 인접한 노드로 가는 비용과
기존의 테이블에 저장되어있던 최소비용을 비교하여 전자가 더 작은 경우 테이블의 최소 비용을 해당 값으로
업데이트한다. 직전 노드 값의 경우 현재 노드로 업데이트 한다.

- D의 경우 B를 거쳐서 가면 5(3+2)이고 기존 테이블의 값은 6이었으므로 테이블을 5로 업데이트한다.
- E의 경우 B를 거쳐서 가면 6(3+3)이고 기존 테이블의 값은 7이었으므로 테이블을 6으로 업데이트 한다.
4번째 반복
2-1. 방문하지 않는 노드들 중 비용이 가장 적은 노드부터 현재 노드로 설정하여 수행한다.
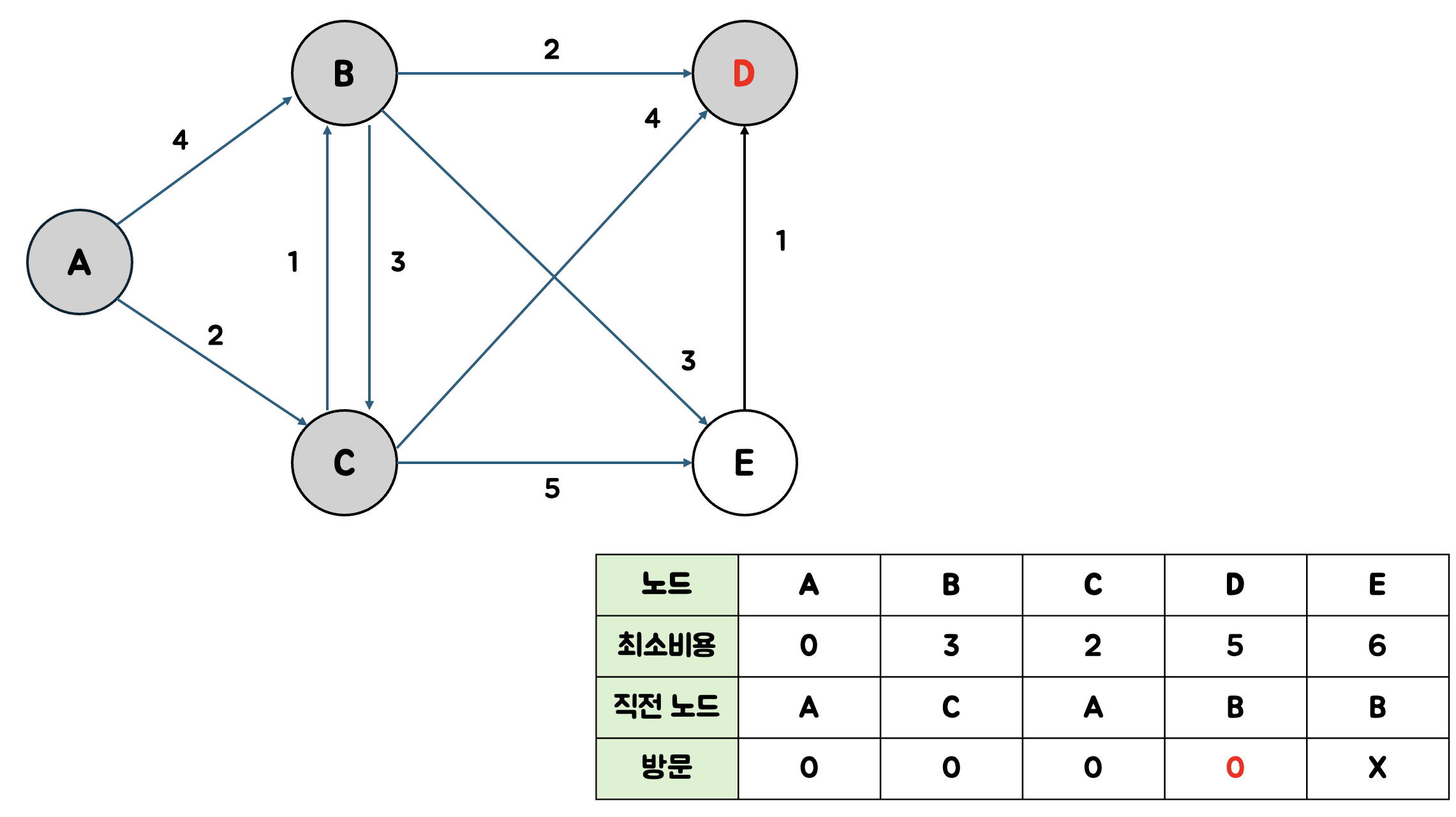
D가 비용이 제일 적으므로 D를 현재 노드로 설정하고 방문처리한다.
D까지의 최소비용은 5이고 최단 경로는 A-C-B-D이다.
2-2. 현재 노드와 방문하지 않은 인접 노드 간의 가중치를 통해 현재 노드를 거쳐 인접한 노드로 가는 비용과
기존의 테이블에 저장되어있던 최소비용을 비교하여 전자가 더 작은 경우 테이블의 최소 비용을 해당 값으로
업데이트한다. 직전 노드 값의 경우 현재 노드로 업데이트 한다.

D에선 인접노드가 없으므로 건너뛴다.
5번째 반복
2-1. 방문하지 않는 노드들 중 비용이 가장 적은 노드부터 현재 노드로 설정하여 수행한다.

E가 비용이 제일 적으므로 E를 현재노드로 하고 방문처리한다.
E까지의 최소비용은 6이고 최단 경로는 A-C-B-E이다.
2-2. 현재 노드와 방문하지 않은 인접 노드 간의 가중치를 통해 현재 노드를 거쳐 인접한 노드로 가는 비용과
기존의 테이블에 저장되어있던 최소비용을 비교하여 전자가 더 작은 경우 테이블의 최소 비용을 해당 값으로
업데이트한다. 직전 노드 값의 경우 현재 노드로 업데이트 한다.

당연하게도 방문하지 않는 노드가 없으므로 업데이트할 것이 없다.
최종결과

참고: 마지막 반복은 사실 생략해도 최종결과를 내는데는 무리가 없다. 그렇기에 실질적인 반복횟수는 노드 - 1번이다.
다익스트라 알고리즘 구현하기
다익스트라 알고리즘의 경우 구현하는 방식이 크게 두 가지가 있다.
첫번째는 배열을 활용하는 간단한 방법이다.
이 방법은 간단하긴 하지만 효율성이 떨어지기 때문에 자주 사용되지 않는다.
두번째는 우선순위 큐를 활용하는 방법이다.
효율성이 배열에 비해 좋기 때문에 선호된다.
코딩테스트에선 최단경로를 묻는 문제보다는 최단거리를 묻는 문제가 많이 나오므로 최단거리만 구현하도록 하겠다.
1. 배열
코드는 다음과 같다.
import java.util.*;
public class Dijkstra_Array {
static class Node {
int vertex;
int weight;
public Node(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
}
static class Graph {
int N; // 노드의 갯수
List<List<Node>> graph;
Graph(int N) {
graph = new ArrayList<>();
for(int i = 0; i < N; i++) {
graph.add(new ArrayList<>());
}
}
public void addEdge(int src, Node node){
graph.get(src).add(node);
}
}
public static int[] dijkstra(List<List<Node>> graph, int start, int n) {
int[] dist = new int[n];
Arrays.fill(dist, Integer.MAX_VALUE);
boolean[] visited = new boolean[n];
dist[start] = 0;
for(int i = 0; i < dist.length; i++) {
int cur_node = getClosestNode(dist, visited);
if(cur_node == -1) break;
visited[cur_node] = true;
for(Node adj: graph.get(cur_node)) {
int adj_node = adj.vertex;
int weight = adj.weight;
if(!visited[adj_node] && dist[adj_node] > dist[cur_node] + weight) {
dist[adj_node] = dist[cur_node] + weight;
}
}
}
return dist;
}
private static int getClosestNode(int[] dist, boolean[] visited) {
int min = Integer.MAX_VALUE;
int closetNode = -1;
for(int i = 0; i < dist.length; i++) {
if(!visited[i] && dist[i] < min) {
min = dist[i];
closetNode = i;
}
}
return closetNode;
}
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addEdge(0, new Node(1, 4));
graph.addEdge(0, new Node(2, 2));
graph.addEdge(1, new Node(2, 3));
graph.addEdge(1, new Node(3, 2));
graph.addEdge(1, new Node(4, 3));
graph.addEdge(2, new Node(1, 1));
graph.addEdge(2, new Node(3, 4));
graph.addEdge(2, new Node(4, 5));
graph.addEdge(4, new Node(3, 1));
System.out.println(Arrays.toString(dijkstra(graph.graph, 0, 5)));
}
}
시간복잡도
- O(N^2)
2. 우선순위 큐
import java.util.*;
public class Dijkstra_Queue {
static class Node {
int vertex;
int weight;
public Node(int vertex, int weight) {
this.vertex = vertex;
this.weight = weight;
}
}
static class Graph {
int N; // 노드의 갯수
List<List<Node>> graph;
Graph(int N) {
graph = new ArrayList<>();
for(int i = 0; i < N; i++) {
graph.add(new ArrayList<>());
}
}
public void addEdge(int src, Node node){
graph.get(src).add(node);
}
}
public static int[] dijkstra(List<List<Node>> graph, int start, int n) {
PriorityQueue<Node> priorityQueue = new PriorityQueue<>((o1, o2) -> Integer.compare(o1.weight, o2.weight));
int[] distance = new int[n];
Arrays.fill(distance, Integer.MAX_VALUE);
boolean[] visited = new boolean[n];
priorityQueue.add(new Node(start, 0));
distance[start] = 0;
while (!priorityQueue.isEmpty()) {
int src = priorityQueue.poll().vertex;
if(visited[src]) continue;
visited[src] = true;
for(Node next: graph.get(src)) {
int next_vertex = next.vertex;
int next_weight = next.weight;
if(distance[next_vertex] > next_weight + distance[src]) {
distance[next_vertex] = next_weight + distance[src];
priorityQueue.add(new Node(next_vertex, next_weight));
}
}
}
return distance;
}
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addEdge(0, new Node(1, 4));
graph.addEdge(0, new Node(2, 2));
graph.addEdge(1, new Node(2, 3));
graph.addEdge(1, new Node(3, 2));
graph.addEdge(1, new Node(4, 3));
graph.addEdge(2, new Node(1, 1));
graph.addEdge(2, new Node(3, 4));
graph.addEdge(2, new Node(4, 5));
graph.addEdge(4, new Node(3, 1));
System.out.println(Arrays.toString(dijkstra(graph.graph, 0, 5)));
}
}
시간복잡도
- O(ElogV)
우선순위 큐에서 데이터를 꺼내거나 넣는 연산은 O(logV)이다.
데이터를 꺼내는 연산은 노드의 개수인 최대 V번 발생하고 데이터를 넣는 연산은 간선의 개수인 최대 E번 발생한다.
따라서 VlogV + ElogV = (V+E)logV이다.
하지만 일반적으로 E>=V이므로 ElogV가 된다.
생각해볼만한 부분이 하나 있다.
해당 코드에서는 큐에서 꺼낸 노드가 이미 방문했다면 그 이하의 작업을 수행하지 않는 부분이 있다.
if(visited[src]) continue;
사실 배열 방식과는 달리 방문여부를 따지지 않아도 알고리즘 결과에는 지장이 없다.
그럼에도 해당 부분을 추가한 이유는 효율성 때문이다.
코드를 실행하다보면 불가피하게 큐에 같은 노드가 여러 번 들어가는 일이 발생한다.
다음은 예시 상황이다.
시작 노드는 0이다.

1. 시작 노드인 0을 우선순위 큐에 넣는다.

2. 큐에서 데이터를 꺼내고 꺼낸 노드의 인접 노드를 우선순위 큐에 넣는다.
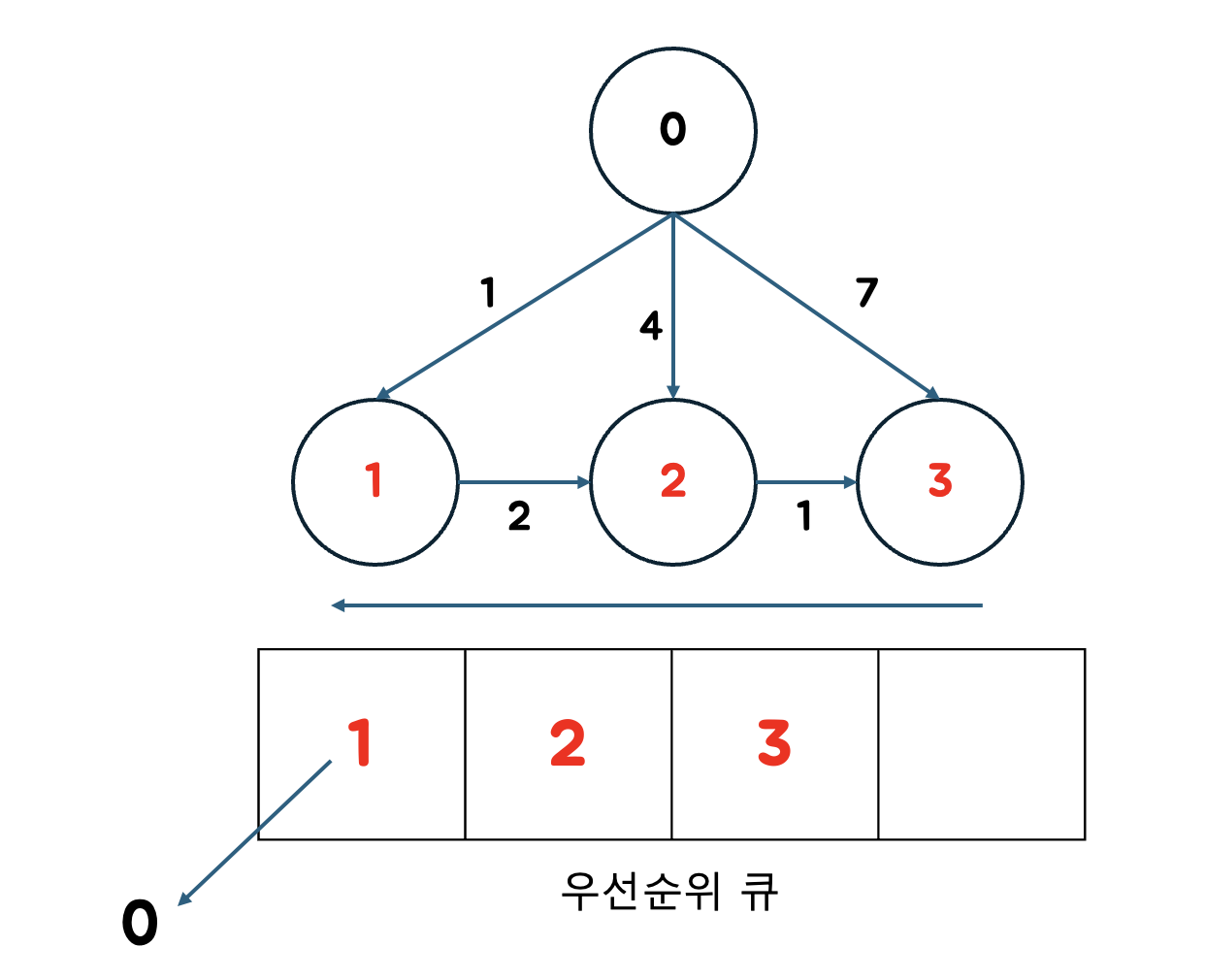
- 0이 큐에서 나왔다.
- 0과 인접한 1, 2, 3을 우선순위 큐에 넣는다.
가중치가 작은 순으로 1, 2, 3 순으로 들어간다.
3. 큐에서 다시 데이터를 꺼내고 꺼낸 노드의 인접 노드를 우선순위 큐에 넣는다.

- 1이 큐에서 나왔다.
- 1과 인접한 2를 우선순위 큐에 넣는다.
가중치가 작은 순으로 2, 3, 2 순으로 들어간다. - 이때 2가 다시 한번 더 큐에 들어가게 된다.
그런데 방문여부를 따지지 않는다면 다음 부분을 불필요하게 여러 번 실행해야한다.
for(Node next: graph.get(src)) {
int next_vertex = next.vertex;
int next_weight = next.weight;
if(distance[next_vertex] > next_weight + distance[src]) {
distance[next_vertex] = next_weight + distance[src];
priorityQueue.add(new Node(next_vertex, next_weight));
}
}
그렇기 때문에 방문여부를 체크해주는 것이다.
한계점
다익스트라 알고리즘은 한가지 한계점이 존재한다.
바로 그래프에 음의 가중치를 가지는 간선이 존재하는 경우 성립하지 않는다는 것이다.
다익스트라에서는 한번 방문한 노드의 최단거리가 수정되는 일은 없다. 왜냐하면 이후에 다른 노드를 거쳐서 방문하더라도 가중치가 증가하지 감소하는 일은 없기 때문이다.
하지만 가중치가 음수라면 최단거리는 충분히 바뀔 수 있다.
따라서 음의 가중치를 가지는 그래프에서 최단거리를 구할 때는 별도의 알고리즘이 필요하다.
그 알고리즘이 바로 벨만 포드 알고리즘이다.
다음 포스트에선 벨만 포드 알고리즘에 대해서 다루도록 하겠다.
'코딩 테스트 > 자료구조 & 알고리즘' 카테고리의 다른 글
| 백트래킹(BackTracking) 알고리즘 (0) | 2024.06.13 |
|---|---|
| 그래프 최단 경로 알고리즘 - 벨만 포드(Bellman-Ford) 알고리즘 (2) | 2024.05.31 |
| 그래프의 탐색(깊이 우선 탐색과 너비 우선탐색) (0) | 2024.05.29 |
| 그래프 (Graph) (0) | 2024.05.29 |
| 상호베타적(서로소) 집합과 유니온 파인드 알고리즘 (0) | 2024.05.24 |
